题目内容
已知向量
=(1,2),
=(2,-3),
=(1,x),若向量
满足
⊥(
+
),则x=( )
| a |
| b |
| c |
| c |
| c |
| a |
| b |
| A、4 | B、2 | C、3 | D、6 |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:由于向量
满足
⊥(
+
),可得
•(
+
)=0,即可解出.
| c |
| c |
| a |
| b |
| c |
| a |
| b |
解答:
解:
+
=(3,-1),
∵向量
满足
⊥(
+
),
∴
•(
+
)=3-x=0,
解得x=3.
故选:C.
| a |
| b |
∵向量
| c |
| c |
| a |
| b |
∴
| c |
| a |
| b |
解得x=3.
故选:C.
点评:本题考查了向量垂直与数量积的关系,属于基础题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
“自然数中a,b,c恰有一个偶数”的否定为( )
| A、自然数a,b,c 都是奇数 |
| B、自然数a,b,c都是偶数 |
| C、自然数a,b,c中至少有两个偶数 |
| D、自然数a,b,c都是奇数或至少有两个偶数 |
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 9×10 |
A、
| ||
B、
| ||
C、
| ||
| D、1 |
已知一个水平放置的平行四边形用斜二测画法作出的直观图是一个边长为1的正方形,则此平行四边形的面积是( )
A、
| ||||
B、
| ||||
C、2
| ||||
| D、4 |
若椭圆的短轴长为4
,它的一个焦点是(2
,0),则该椭圆的标准方程是( )
| 5 |
| 15 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
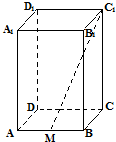 如图,正四棱柱(底面是正方形的直棱柱)ABCD-A1B1C1D1的底面边长为1,高为2,M为线段AB的中点,设异面直线CD与MC1所成角为θ,则tanθ=( )
如图,正四棱柱(底面是正方形的直棱柱)ABCD-A1B1C1D1的底面边长为1,高为2,M为线段AB的中点,设异面直线CD与MC1所成角为θ,则tanθ=( )