题目内容
从装有红球、白球和黑球各2个的口袋内一次取出2个球,给出以下事件:
①两球都不是白球;
②两球中恰有一白球;
③两球中至少有一个白球.
其中与事件“两球都为白球”互斥而非对立的事件是( )
①两球都不是白球;
②两球中恰有一白球;
③两球中至少有一个白球.
其中与事件“两球都为白球”互斥而非对立的事件是( )
| A、①② | B、①③ | C、②③ | D、①②③ |
考点:互斥事件与对立事件
专题:操作型,概率与统计
分析:结合互斥事件和对立事件的定义,即可得出结论.
解答:
解:根据题意,结合互斥事件、对立事件的定义可得,事件“两球都为白球”和事件“两球都不是白球”;事件“两球都为白球”和事件“两球中恰有一白球”;不可能同时发生,故它们是互斥事件.
但这两个事件不是对立事件,因为他们的和事件不是必然事件.
故选A.
但这两个事件不是对立事件,因为他们的和事件不是必然事件.
故选A.
点评:本题考查互斥事件与对立事件.首先要求理解互斥事件和对立事件的定义,理解互斥事件与对立事件的联系与区别.同时要能够准确列举某一事件所包含的基本事件.属简单题.

练习册系列答案
相关题目
若椭圆的短轴长为4
,它的一个焦点是(2
,0),则该椭圆的标准方程是( )
| 5 |
| 15 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知数列{an}共有m项,定义{an}的所有项和为S(1),第二项及以后所有项的和为S(2),第三项及以后所有项的和为S(3),…,第n项及以后所有项的和为S(n).若S(n)是首项为2,公比为
的等比数列的前n项和,则当n<m时,an=( )
| 1 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知x>0,y>0,且2x+y=1,则
+
的最小值为( )
| 1 |
| x |
| 1 |
| y |
| A、3 | ||
B、2+3
| ||
C、3+2
| ||
D、2-3
|
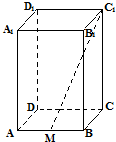 如图,正四棱柱(底面是正方形的直棱柱)ABCD-A1B1C1D1的底面边长为1,高为2,M为线段AB的中点,设异面直线CD与MC1所成角为θ,则tanθ=( )
如图,正四棱柱(底面是正方形的直棱柱)ABCD-A1B1C1D1的底面边长为1,高为2,M为线段AB的中点,设异面直线CD与MC1所成角为θ,则tanθ=( )