题目内容
某同学在一次研究性学习中发现,以下五个式子的值都等于同一个常数.
(1)sin213°+cos217°-sin13°cos17°
(2)sin215°+cos215°-sin15°cos15°
(3)sin218°+cos212°-sin18°cos12°
(4)sin2(-18°)+cos248°-sin2(-18°)cos248°
(5)sin2(-25°)+cos255°-sin2(-25°)cos255°
则这个常数为( )
(1)sin213°+cos217°-sin13°cos17°
(2)sin215°+cos215°-sin15°cos15°
(3)sin218°+cos212°-sin18°cos12°
(4)sin2(-18°)+cos248°-sin2(-18°)cos248°
(5)sin2(-25°)+cos255°-sin2(-25°)cos255°
则这个常数为( )
A、
| ||
B、
| ||
| C、1 | ||
| D、0 |
考点:归纳推理
专题:计算题,推理和证明
分析:选择(2),计算可得这个常数的值.
解答:
解:选择(2),计算如下:
sin215°+cos215°-sin15°cos15°=1-
sin30°=
,故这个常数为
,
故选:A.
sin215°+cos215°-sin15°cos15°=1-
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 4 |
故选:A.
点评:本题主要考查二倍角公式的应用,考查归纳推理以及计算能力,属于基础题.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
对于任意的实数a,b,c,d有如下说法,其中正确的个数为 ( )
(1)若a>b,c>d,则a+c>b+d.
(2)若ac2>bc2,则a>b.
(3)若a>b,则ac2>bc2.
(4)若a>b,c>d,则ac>bd.
(1)若a>b,c>d,则a+c>b+d.
(2)若ac2>bc2,则a>b.
(3)若a>b,则ac2>bc2.
(4)若a>b,c>d,则ac>bd.
| A、4 | B、3 | C、2 | D、1 |
已知函数f(x)是定义在R上的可导函数,且f(-1)=2,f′(x)>2,则不等式f(x)>2x+4的解集为( )
| A、(-∞,-1) |
| B、(-1,+∞) |
| C、(-1,0) |
| D、(0,+∞) |
已知函数y=f(x)的定义域为R,当x<0时,f(x)>1,且对任意的实数x,y∈R,等式f(x)f(y)=f(x+y)成立.若数列{an}满足a1=f(0),且f(an+1)=
(n∈N*),则a2013的值为( )
| 1 |
| f(-2-an) |
| A、4026 | B、4025 |
| C、4024 | D、4023 |
已知一个水平放置的平行四边形用斜二测画法作出的直观图是一个边长为1的正方形,则此平行四边形的面积是( )
A、
| ||||
B、
| ||||
C、2
| ||||
| D、4 |
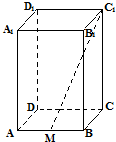 如图,正四棱柱(底面是正方形的直棱柱)ABCD-A1B1C1D1的底面边长为1,高为2,M为线段AB的中点,设异面直线CD与MC1所成角为θ,则tanθ=( )
如图,正四棱柱(底面是正方形的直棱柱)ABCD-A1B1C1D1的底面边长为1,高为2,M为线段AB的中点,设异面直线CD与MC1所成角为θ,则tanθ=( )