题目内容
13.若关于x的不等式4x-logax<0在区间(0,$\frac{1}{2}$]上恒成立,则实数a的取值范围是($\frac{\sqrt{2}}{2}$,1).分析 若关于x的不等式4x-logax<0在区间(0,$\frac{1}{2}$]上恒成立,则y=logax的图象恒在y=4x的图象的上方,在同一坐标系中,分析画出指数和对数函数的图象,分析可得答案.
解答 解:当0<x≤$\frac{1}{2}$时,函数y=4x的图象如下图所示: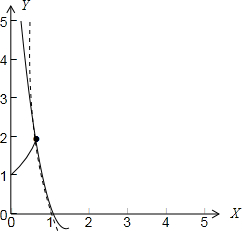
若不等式4x-logax<0在区间(0,$\frac{1}{2}$]上恒成立,即不等式4x<logax恒成立,
则y=logax的图象恒在y=4x的图象的上方(如图中虚线所示)
∵y=logax的图象与y=4x的图象交于($\frac{1}{2}$,2)点时,a=$\frac{\sqrt{2}}{2}$
故虚线所示的y=logax的图象对应的底数a应满足$\frac{\sqrt{2}}{2}$<a<1
故答案为:($\frac{\sqrt{2}}{2}$,1)
点评 本题以指数函数与对数函数图象与性质为载体考查了函数恒成立问题,其中熟练掌握指数函数和对数函数的图象与性质是解答本题的关键.

练习册系列答案
相关题目
3.执行如图所示的程序框图,则输出的k值为( )


| A. | 7 | B. | 9 | C. | 11 | D. | 13 |
1.下列四组函数中表示同一函数的是( )
| A. | f(x)=x,g(x)=($\sqrt{x}$)2 | B. | f(x)=x2,g(x)=(x+1)2 | C. | f(x)=0,g(x)=$\sqrt{x-1}+\sqrt{1-x}$ | D. | f(x)=$\sqrt{{x}^{2}}$,g(x)=|x| |
8.函数$f(x)=\frac{1}{x^2}$的单调递增区间为( )
| A. | (-∞,0] | B. | [0,+∞) | C. | (0,+∞) | D. | (-∞,0) |
18.若命题“p∨q”为真,且“¬p”为真,则( )
| A. | p或q为假 | B. | q假 | C. | q真 | D. | 不能判断q的真假 |
5.若二次函数y=-x2+2x+2,当x∈[a,3]时,y∈[-1,3],则实数a的取值范围为( )
| A. | [-1,3] | B. | [-1,1] | C. | (-1,1) | D. | [1,3] |
3.在(x2-x)5的展开式中,含x7项的系数为( )
| A. | -10 | B. | 10 | C. | -15 | D. | 15 |