题目内容
2.若函数$f(x)=\frac{1}{|x|-2}-m$只有一个零点,则实数m=-2.分析 由题意函数$f(x)=\frac{1}{|x|-2}-m$只有一个零点,方程$\frac{1}{|x|-2}=m$只有一个实数根,函数y=$\frac{1}{|x|-2}$的图象和直线 y=k只有一个交点,数形结合可得m的值.
解答 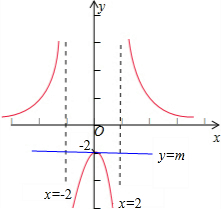 解:∵函数$f(x)=\frac{1}{|x|-2}-m$只有一个零点,
解:∵函数$f(x)=\frac{1}{|x|-2}-m$只有一个零点,
∴方程$\frac{1}{|x|-2}=m$只有一个实数根,
∴函数y=$\frac{1}{|x|-2}$=$\left\{\begin{array}{l}{\frac{1}{x-2},x<-2,x>2}\\{\frac{1}{2-x},-2<x<2}\end{array}\right.$的图象和直线 y=m只有一个交点,
画出函数y=$\frac{1}{|x|-2}$的图象的单调性示意图,数形结合可得
m=-2,
故答案为:-2.
点评 本题主要考查函数的零点与方程的根的关系,体现了转化以及数形结合的数学学思想,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.函数y=log3x(x≥1)的值域是( )
| A. | [2,+∞) | B. | (3,+∞) | C. | [0,+∞) | D. | R |