题目内容
函数f(x)=sin4x+cos2x-1(x∈R)的值域为 .
考点:三角函数的最值
专题:计算题,三角函数的求值,三角函数的图像与性质
分析:把函数解析式中的两项分别利用二倍角的余弦函数公式化简,整理后再利用二倍角的余弦函数公式,把解析式化为一个角的余弦函数,再由余弦函数的值域即可得到.
解答:
解:y=sin4x+cos2x-1
=(
)2+
-1
=
-1=
+
-1=
cos4x-
,
当cos4x=1时,y取最大值0,cos2x=-1时,y取最小值-
-
=-
.
故值域为[-
,0],
故答案为:[-
,0]
=(
| 1-cos2x |
| 2 |
| 1+cos2x |
| 2 |
=
| 3+cos22x |
| 4 |
| 3 |
| 4 |
| 1+cos4x |
| 8 |
| 1 |
| 8 |
| 1 |
| 8 |
当cos4x=1时,y取最大值0,cos2x=-1时,y取最小值-
| 1 |
| 8 |
| 1 |
| 8 |
| 1 |
| 4 |
故值域为[-
| 1 |
| 4 |
故答案为:[-
| 1 |
| 4 |
点评:此题考查了三角函数的值域及其求法,涉及的知识有:二倍角的余弦函数公式,以及三角函数的周期公式,灵活运用二倍角的余弦函数公式把函数解析式化为一个角的三角函数是解此类题的关键.

练习册系列答案
相关题目
已知命题p:对任意x∈R,总有x2≥0; q:x=2是方程x+3=0的根,则下列命题为真命题的是( )
| A、¬p∧q | B、p∧¬q |
| C、¬p∧¬q | D、p∧q |
已知数列{an}为等差数列,Sn是数列{an}的前n项和,a1+a6+a11=4π,则sin(S11)的值为( )
A、
| ||||
B、±
| ||||
C、
| ||||
D、-
|
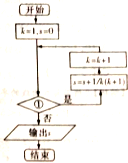
如图是求
+
+
+…+
的值的程序框图,则判断框①中应填( )
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 99×100 |

| A、k≤99? |
| B、k<99? |
| C、k≤100? |
| D、k<98? |