题目内容
下列命题中,真命题有 (写出所有真命题的序号)
(1)在△ABC中,“A>B”是“sinA>sinB”的充要条件;
(2)点(
,0)为函数f(x)=tan(2x+
)的一个对称中心;
(3)若|
|=1,|
|=2,向量
与向量
的夹角为120°,则
在向量
上的投影为1;
(4)?a>0,函数f(x)=ln2x+lnx-a有零点.
(1)在△ABC中,“A>B”是“sinA>sinB”的充要条件;
(2)点(
| π |
| 8 |
| π |
| 4 |
(3)若|
| a |
| b |
| a |
| b |
| b |
| a |
(4)?a>0,函数f(x)=ln2x+lnx-a有零点.
考点:命题的真假判断与应用
专题:简易逻辑
分析:根据正弦定理,及三角形的性质,可判断(1);根据正切函数的对称性,可判断(2);根据向量投影的定义,可判断(3);根据对数函数的图象和性质,二次函数的图象和性质,可判断(4).
解答:
解:(1)解:sinA>sinB?2RsinA>2RsinB?a>b?A>B(其中R为△ABC外接圆半径),故(1)正确;
(2)函数f(x)=tan(2x+
)的对称中心坐标为(
-
,0),k∈Z,当k=1时,点(
,0)为函数f(x)=tan(2x+
)的一个对称中心,故(2)正确;
(3)若|
|=1,|
|=2,向量
与向量
的夹角为120°,则
在向量
上的投影为|
|cos120°=-1,故(3)错误;
(4)当a>0时,令t=lnx,则y=t2+t-a,由△=1+4a>0可得方程有两相异的根,存在t=lnx,使f(x)=ln2x+lnx-a=0成立,即函数f(x)=ln2x+lnx-a有零点.
故正确的命题有:(1),(2),(4),
故答案为:(1),(2),(4)
(2)函数f(x)=tan(2x+
| π |
| 4 |
| kπ |
| 4 |
| π |
| 8 |
| π |
| 8 |
| π |
| 4 |
(3)若|
| a |
| b |
| a |
| b |
| b |
| a |
| b |
(4)当a>0时,令t=lnx,则y=t2+t-a,由△=1+4a>0可得方程有两相异的根,存在t=lnx,使f(x)=ln2x+lnx-a=0成立,即函数f(x)=ln2x+lnx-a有零点.
故正确的命题有:(1),(2),(4),
故答案为:(1),(2),(4)
点评:本题考查的知识点是命题的真假判断与应用,熟练掌握正弦定理,正切函数的图象和性质,对数函数的图象和性质,二次函数的图象和性质,向量投影的定义,是解答的关键.

练习册系列答案
相关题目
若函数f(x)=sin2x-
(x∈R),则f(x)是( )
| 1 |
| 2 |
A、最小正周期为
| ||
| B、最小正周期为π的奇函数 | ||
| C、最小正周期为2π的偶函数 | ||
| D、最小正周期为π的偶函数 |
下列命题中为假命题的是( )
| A、?x∈R,logax=-1(a>0,a≠1) |
| B、?x∈R,tanx=2014 |
| C、?x∈R,ax>0(a>0,a≠1) |
| D、?x∈R,x2+ax+a2>0(a∈R) |
已知:p:x≥k,q:
<0,如果p是q的充分不必要条件,则k的取值范围是( )
| 2-x |
| x+1 |
| A、[2,+∞) |
| B、(2,+∞) |
| C、[1,+∞) |
| D、(-∞,-1] |
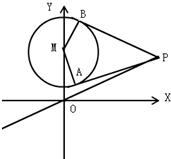 如图,已知圆M:x2+(y-4)2=4,直线l的方程为x-2y=0,点P是直线l上一动点,过点P作圆的切线PA、PB,切点为A、B.
如图,已知圆M:x2+(y-4)2=4,直线l的方程为x-2y=0,点P是直线l上一动点,过点P作圆的切线PA、PB,切点为A、B.