题目内容
已知两个实数a,b(a≠b),满足aea=beb,命题p:lna+a=lnb+b;命题q:(a+1)(b+1)<0.则下面命题正确的是( )
| A、p真q假 | B、p假q真 |
| C、p真q真 | D、p假q假 |
考点:复合命题的真假
专题:简易逻辑
分析:由已知aea=beb可联想构造函数y=xex,求导后由函数的单调性结合x<-1时y恒小于0可得a,b均小于0而且一个比-1大一个比-1小,由此可以得到选项.
解答:
解:构造函数y=xex,
则y′=ex+xex=(x+1)ex,
∵ex>0,
∴当x<-1时,y′<0,函数y=xex为减函数,
当x>-1时,y′>0,函数y=xex为增函数,
要使aea=beb,
则a,b必须均小于0而且一个比-1大一个比-1小,
∴命题p为假命题,命题q为真命题.
故选:B.
则y′=ex+xex=(x+1)ex,
∵ex>0,
∴当x<-1时,y′<0,函数y=xex为减函数,
当x>-1时,y′>0,函数y=xex为增函数,
要使aea=beb,
则a,b必须均小于0而且一个比-1大一个比-1小,
∴命题p为假命题,命题q为真命题.
故选:B.
点评:本题考查命题的真假判断与应用,训练了函数构造法,考查了利用导数研究函数的单调性,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在等差数列{an}中,已知a2与a4是方程x2-6x+8=0的两个根,若a4>a2,则a2014=( )
| A、2012 | B、2013 |
| C、2014 | D、2015 |
设双曲线C:
-
=1(b>0)的上、下焦点分别为F1,F2,且双曲线C的一条渐近线的一个方向向量
=(3,4),过下焦点F1的直线l交双曲线的下支于A,B两点,则|BF2|+AF2|的最小值为( )
| y2 |
| 16 |
| x2 |
| b2 |
| v |
A、
| ||
B、
| ||
| C、19 | ||
| D、41 |
 如图,在正方体ABCD-A1B1C1D1中,点P是上底面A1B1C1D1内一动点,则三棱锥P-BCD的正视图与侧视图的面积之比为( )
如图,在正方体ABCD-A1B1C1D1中,点P是上底面A1B1C1D1内一动点,则三棱锥P-BCD的正视图与侧视图的面积之比为( )| A、1:1 | B、2:1 |
| C、2:3 | D、3:2 |
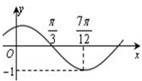 f(x)=Acos(ωx+φ)(A,ω>0)的图象如图所示,为得到g(x)=-Asin(ωx+
f(x)=Acos(ωx+φ)(A,ω>0)的图象如图所示,为得到g(x)=-Asin(ωx+| π |
| 6 |
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|