题目内容
已知等差数列{an}中,a3+a4=a12,a1+a2=10,则a2+a4+…a100的值等于( )
| A、1300 | ||
| B、1350 | ||
| C、2650 | ||
D、
|
考点:等差数列的性质
专题:等差数列与等比数列
分析:设等差数列{an}的公差,由已知列式求出首项和公差,代入a2+a4+…a100得答案.
解答:
解:设等差数列{an}的公差为d,
由a3+a4=a12,a1+a2=10,得:
,解得:
.
∴a2=a1+d=
+
=
.
∴a2+a4+…a100=50×
+
×
=
.
故选:D.
由a3+a4=a12,a1+a2=10,得:
|
|
∴a2=a1+d=
| 60 |
| 13 |
| 10 |
| 13 |
| 70 |
| 13 |
∴a2+a4+…a100=50×
| 70 |
| 13 |
| 50×49 |
| 2 |
| 20 |
| 13 |
| 28000 |
| 13 |
故选:D.
点评:本题考查了等差数列的通项公式,考查了等差数列的性质,是基础的计算题.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
 如图,在正方体ABCD-A1B1C1D1中,点P是上底面A1B1C1D1内一动点,则三棱锥P-BCD的正视图与侧视图的面积之比为( )
如图,在正方体ABCD-A1B1C1D1中,点P是上底面A1B1C1D1内一动点,则三棱锥P-BCD的正视图与侧视图的面积之比为( )| A、1:1 | B、2:1 |
| C、2:3 | D、3:2 |
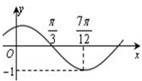 f(x)=Acos(ωx+φ)(A,ω>0)的图象如图所示,为得到g(x)=-Asin(ωx+
f(x)=Acos(ωx+φ)(A,ω>0)的图象如图所示,为得到g(x)=-Asin(ωx+| π |
| 6 |
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|
执行如图所示的程序框图,若输出的结果为21,则判断框中应填( )


| A、i<5 | B、i<6 |
| C、i<7 | D、i<8 |
在平面直角坐标系xOy中,圆C的方程为x2+y2-4x=0.若直线y=k(x+1)上存在一点P,使过P所作的圆的两条切线相互垂直,则实数k的取值范围是( )
A、(-∞,-2
| ||||||||
B、[-2
| ||||||||
C、[-
| ||||||||
D、(-∞,-2
|
设△ABC的内角A、B、C所对边的长分别为a、b、c,若a,b,c成等差数列,且5sinA=3sinB,则角C为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
