题目内容
公差不为零的等差数列{an}的前n项和为Sn,若a3是a2与a6的等比中项,S4=8,则S6=( )
| A、18 | B、24 | C、60 | D、90 |
考点:等差数列的性质
专题:计算题,等差数列与等比数列
分析:利用a3是a2与a6的等比中项,可得d=-2a1,利用S4=8,求出a1=-1,d=2,即可求出S6.
解答:
解:由题意,∵a3是a2与a6的等比中项,
∴(a1+2d)2=(a1+d)(a1+5d),
∴2a1d+d2=0,
∵d≠0,
∴d=-2a1,
∵S4=8,
∴4a1+6d=8
解得a1=-1,d=2,
故S6=6a1+15d=-6+30=24.
故选:B.
∴(a1+2d)2=(a1+d)(a1+5d),
∴2a1d+d2=0,
∵d≠0,
∴d=-2a1,
∵S4=8,
∴4a1+6d=8
解得a1=-1,d=2,
故S6=6a1+15d=-6+30=24.
故选:B.
点评:本题考查等比数列的性质,考查等差数列的通项与求和,考查学生的计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在正方体ABCD-A1B1C1D1中,点P是上底面A1B1C1D1内一动点,则三棱锥P-BCD的正视图与侧视图的面积之比为( )
如图,在正方体ABCD-A1B1C1D1中,点P是上底面A1B1C1D1内一动点,则三棱锥P-BCD的正视图与侧视图的面积之比为( )| A、1:1 | B、2:1 |
| C、2:3 | D、3:2 |
执行如图所示程序框图,则输出的S的值为( )


| A、21 | B、25 | C、45 | D、93 |
若直线xcosθ+ysinθ+1=0与圆(x+1)2+(y-1)2=1相切,且θ为锐角,则该直线的斜率是( )
| A、1 | ||
B、-
| ||
| C、-1 | ||
D、
|
已知
与
的夹角为
,且
•
=
,则|
-
|的最小值为( )
| a |
| b |
| π |
| 6 |
| a |
| b |
| 3 |
| a |
| b |
A、4-2
| ||
B、
| ||
C、
| ||
D、4+2
|
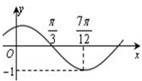 f(x)=Acos(ωx+φ)(A,ω>0)的图象如图所示,为得到g(x)=-Asin(ωx+
f(x)=Acos(ωx+φ)(A,ω>0)的图象如图所示,为得到g(x)=-Asin(ωx+| π |
| 6 |
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|
执行如图所示的程序框图,若输出的结果为21,则判断框中应填( )


| A、i<5 | B、i<6 |
| C、i<7 | D、i<8 |
