题目内容
已知集合M={x|x2+2x-3＞0}，N={x|y=
}，则（∁RM）∪N为（ ）
| ||
| ln(2x-x2) |
| A、[-3，2） |
| B、（-2，3] |
| C、[-3，1）∪（1，2） |
| D、[-1，2） |
考点：交、并、补集的混合运算
专题：集合
分析：求出M中不等式的解集，确定出M，求出M的补集，求出N中x的范围确定出N，找出M补集与N的并集即可．
解答：
解：由M中的不等式变形得：（x-1）（x+3）＞0，
解得：x＜-3或x＞1，即M=（-∞，-3）∪（1，+∞），
∴∁RM=[-3，1]，
由N中y=
，得到
，
解得：1＜x＜2，即N=（1，2），
则（∁RM）∪N=[-3，2）．
故选：A．
解得：x＜-3或x＞1，即M=（-∞，-3）∪（1，+∞），
∴∁RM=[-3，1]，
由N中y=
| ||
| ln(2x-x2) |
|
解得：1＜x＜2，即N=（1，2），
则（∁RM）∪N=[-3，2）．
故选：A．
点评：此题考查了交、并、补集的混合运算，熟练掌握各自的定义是解本题的关键．
练习册系列答案
寒假大串联黄山书社系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
设双曲线C：
-
=1（b＞0）的上、下焦点分别为F1，F2，且双曲线C的一条渐近线的一个方向向量
=（3，4），过下焦点F1的直线l交双曲线的下支于A，B两点，则|BF2|+AF2|的最小值为（ ）
| y2 |
| 16 |
| x2 |
| b2 |
| v |
A、
| ||
B、
| ||
| C、19 | ||
| D、41 |
如图，在正方体ABCD-A1B1C1D1中，点P是上底面A1B1C1D1内一动点，则三棱锥P-BCD的正视图与侧视图的面积之比为（ ）| A、1：1 | B、2：1 |
| C、2：3 | D、3：2 |
复数z1=2+i，z2=
在复平面上分别对应点A，B，则∠AOB=（ ）
| 1 |
| 3+i |
A、
| ||
B、
| ||
C、
| ||
D、
|
执行如图所示程序框图，则输出的S的值为（ ）
| A、21 | B、25 | C、45 | D、93 |
若直线xcosθ+ysinθ+1=0与圆（x+1）2+（y-1）2=1相切，且θ为锐角，则该直线的斜率是（ ）
| A、1 | ||
B、-
| ||
| C、-1 | ||
D、
|
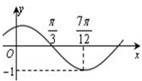f（x）=Acos（ωx+φ）（A，ω＞0）的图象如图所示，为得到g（x）=-Asin（ωx+| π |
| 6 |
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|
设△ABC的内角A、B、C所对边的长分别为a、b、c，若a，b，c成等差数列，且5sinA=3sinB，则角C为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|