题目内容
已知点F是椭圆
+y2=1（a＞0）的右焦点，动点P到点F的距离等于到直线x=-a的距离．
（1）求点P的轨迹C的方程；
（2）设过点F任作一直线与点P的轨迹交于A、B两点，直线OA、OB与直线x=-a分别交于点S、T（O为坐标原点），试判断
•
是否为定值？若是，求出这个定值；若不是，请说明理由．
| x2 |
| 1+a2 |
（1）求点P的轨迹C的方程；
（2）设过点F任作一直线与点P的轨迹交于A、B两点，直线OA、OB与直线x=-a分别交于点S、T（O为坐标原点），试判断
| FS |
| FT |
考点：直线与圆锥曲线的综合问题
专题：圆锥曲线中的最值与范围问题
分析：（1）由已和条件推导出点P的轨迹C是以点F为焦点、直线x=-a为准线的抛物线，由此能求出C的方程．
（2）设直线AB的方程为x=ty+a，A(
， y1)、B(
， y2)，由已知条件推导出
•
=4a2+
．由
，得y2-4aty-4a2=0，由此能求出
•
的值是定值0．
（2）设直线AB的方程为x=ty+a，A(
| y12 |
| 4a |
| y22 |
| 4a |
| FS |
| FT |
| 16a4 |
| y1y2 |
|
| FS |
| FT |
解答：
解：（1）∵椭圆
+y2=1右焦点F的坐标为（a，0），…（1分）
由抛物线定义知，
点P的轨迹C是以点F为焦点、直线x=-a为准线的抛物线，…（3分）
∴C的方程为y2=4ax．…（5分）
（2）设直线AB的方程为x=ty+a，A(
， y1)、B(
， y2)，
则lOA：y=
x，lOB：y=
x．…（6分）
由
，得S(-a， -
)，
同理得T(-a， -
)．…（8分）
∴
=(-2a， -
)，
=(-2a， -
)，
则
•
=4a2+
．…（9分）
由
，得y2-4aty-4a2=0，∴y1y2=-4a2．…（11分）
则
•
=4a2+
=4a2-4a2=0．…（13分）
∴
•
的值是定值，且定值为0．…（14分）
| x2 |
| 1+a2 |
由抛物线定义知，
点P的轨迹C是以点F为焦点、直线x=-a为准线的抛物线，…（3分）
∴C的方程为y2=4ax．…（5分）
（2）设直线AB的方程为x=ty+a，A(
| y12 |
| 4a |
| y22 |
| 4a |
则lOA：y=
| 4a |
| y1 |
| 4a |
| y2 |
由
|
| 4a2 |
| y1 |
同理得T(-a， -
| 4a2 |
| y2 |
∴
| FS |
| 4a2 |
| y1 |
| FT |
| 4a2 |
| y2 |
则
| FS |
| FT |
| 16a4 |
| y1y2 |
由
|
则
| FS |
| FT |
| 16a4 |
| (-4a2) |
∴
| FS |
| FT |
点评：本题考查点的轨迹方程的求法，考查向量的数量积是否为定值的判断与求法，解题时要认真审题，注意抛物线与直线的位置关系的灵活运用．
练习册系列答案
相关题目
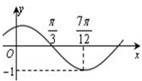f（x）=Acos（ωx+φ）（A，ω＞0）的图象如图所示，为得到g（x）=-Asin（ωx+| π |
| 6 |
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|
设△ABC的内角A、B、C所对边的长分别为a、b、c，若a，b，c成等差数列，且5sinA=3sinB，则角C为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
