题目内容
某几何体的三视图如图所示,则它的体积是( )


| A、5 | ||
| B、6 | ||
C、
| ||
D、
|
考点:由三视图求面积、体积
专题:计算题,空间位置关系与距离
分析:几何体是两个三棱锥的组合体,判断三棱锥的结构特征,结合直观图求相关几何量的数据,把数据代入棱锥的体积公式计算.
解答:
解:由三视图知:几何体是两个三棱锥的组合体,如图:
其中SA⊥平面ABC,GC⊥平面ABC,AD=3,CD=1,SA=4,GC=2,
BD⊥AC,BD=2,
∴几何体的体积V=
×
×3×2×4+
×
×2×1×2=4+
=
.
故选:C.

其中SA⊥平面ABC,GC⊥平面ABC,AD=3,CD=1,SA=4,GC=2,
BD⊥AC,BD=2,
∴几何体的体积V=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 3 |
| 14 |
| 3 |
故选:C.

点评:本题考查了由三视图求几何体的体积,根据三视图判断几何体的形状及数据所队员们的几何量是解题的关键.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
在等差数列{an}中,已知a2与a4是方程x2-6x+8=0的两个根,若a4>a2,则a2014=( )
| A、2012 | B、2013 |
| C、2014 | D、2015 |
执行如图所示程序框图,则输出的S的值为( )


| A、21 | B、25 | C、45 | D、93 |
已知
与
的夹角为
,且
•
=
,则|
-
|的最小值为( )
| a |
| b |
| π |
| 6 |
| a |
| b |
| 3 |
| a |
| b |
A、4-2
| ||
B、
| ||
C、
| ||
D、4+2
|
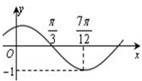 f(x)=Acos(ωx+φ)(A,ω>0)的图象如图所示,为得到g(x)=-Asin(ωx+
f(x)=Acos(ωx+φ)(A,ω>0)的图象如图所示,为得到g(x)=-Asin(ωx+| π |
| 6 |
A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|
在△ABC中,AC=
,AB=3,BC=2,M,N,P分别为AC,AB,BC中点,将△ABC沿MN,NP,MP折起得到三棱锥S-MNP,三棱锥S-MNP外接球的表面积为( )
| 7 |
| A、10π | ||
| B、8π | ||
| C、5π | ||
D、
|
执行如图所示的程序框图,若输出的结果为21,则判断框中应填( )


| A、i<5 | B、i<6 |
| C、i<7 | D、i<8 |
在平面直角坐标系xOy中,圆C的方程为x2+y2-4x=0.若直线y=k(x+1)上存在一点P,使过P所作的圆的两条切线相互垂直,则实数k的取值范围是( )
A、(-∞,-2
| ||||||||
B、[-2
| ||||||||
C、[-
| ||||||||
D、(-∞,-2
|