题目内容
5.圆的方程是x2+y2-6x-4y+8=0,则过圆上一点P(2,0)的切线方程是x+2y-2=0.分析 化圆的一般方程为标准方程,求出圆心坐标,进一步求出连接圆心和P点的连线的斜率,得到切线的斜率,代入直线方程的点斜式得答案.
解答 解:由x2+y2-6x-4y+8=0,得(x-3)2+(y-2)2=5,
∴圆心坐标为C(3,2),又P(2,0),
则${k}_{CP}=\frac{2-0}{3-2}=2$,
∴过圆上一点P(2,0)的切线方程是y-0=$-\frac{1}{2}$(x-2),即x+2y-2=0.
故答案为:x+2y-2=0.
点评 本题考查圆的切线方程,训练了直线方程点斜式的应用,是基础题.

练习册系列答案
相关题目
17.已知k∈Z,$\overrightarrow{AB}$=(k,1),$\overrightarrow{BC}$=(k-2,-3),若|$\overrightarrow{AB}$|≤$\sqrt{17}$,则∠ABC是直角的概率是( )
| A. | $\frac{4}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{9}$ | D. | $\frac{1}{9}$ |
17.某高校一专业在一次自主招生中,对20名已经选拔入围的学生进行语言表达能力和逻辑思维能力测试,结果如表:
由于部分数据丢失,只知道从这20名参加测试的学生中随机抽取一人,抽到语言表达能力优秀或逻辑思维能力优秀的学生的概率为$\frac{2}{5}$.
(1)求m,n的值;
(2)从参加测试的语言表达能力良好的学生中任意抽取2名,求其中至少有一名逻辑思维能力优秀的学生的概率.
| 语言表达能力 人数 逻辑思维能力 | 一般 | 良好 | 优秀 |
| 一般 | 2 | 2 | 1 |
| 良好 | 4 | m | 1 |
| 优秀 | 1 | 3 | n |
(1)求m,n的值;
(2)从参加测试的语言表达能力良好的学生中任意抽取2名,求其中至少有一名逻辑思维能力优秀的学生的概率.
13.复数z满足z(2-i)=3+i,则$\overline z$=( )
| A. | 1-i | B. | 1+i | C. | -1-i | D. | -1+i |
10.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点与抛物线y2=2px(p>0)的焦点重合,若抛物线的准线交双曲线于A、B两点,当|AB|=4a时,此双曲线的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
17.平面直角坐标系xOy中,双曲线C1:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的渐近线与抛物线C2:y2=2px(p>0)交于点O,A,B,若△OAB的重心为C2的焦点,则C1的渐近线方程为( )
| A. | y=±$\frac{\sqrt{6}}{4}$x | B. | y=±$\frac{2\sqrt{6}}{3}$x | C. | y=±2$\sqrt{2}$x | D. | y=±$\frac{2\sqrt{3}}{3}$x |
14.已知双曲线$\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1的左右焦点分别为F1、F2,点P为双曲线上一点,△F1PF2的内切圆圆心为M,若S${\;}_{△{F}_{1}PM}$=S${\;}_{△{F}_{2}PM}$+8,那么S${\;}_{△{F}_{1}M{F}_{2}}$( )
| A. | 2$\sqrt{7}$ | B. | 6 | C. | 8 | D. | 10 |
14.已知p:a>4,q:方程$\frac{{x}^{2}}{4-a}$-$\frac{{y}^{2}}{1-a}$=1表示双曲线,则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
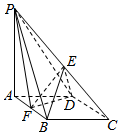 如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,AB=2,PA=3,PA⊥平面ABCD,E是PC的中点,F是AB的中点.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,AB=2,PA=3,PA⊥平面ABCD,E是PC的中点,F是AB的中点.