题目内容
17.某高校一专业在一次自主招生中,对20名已经选拔入围的学生进行语言表达能力和逻辑思维能力测试,结果如表:| 语言表达能力 人数 逻辑思维能力 | 一般 | 良好 | 优秀 |
| 一般 | 2 | 2 | 1 |
| 良好 | 4 | m | 1 |
| 优秀 | 1 | 3 | n |
(1)求m,n的值;
(2)从参加测试的语言表达能力良好的学生中任意抽取2名,求其中至少有一名逻辑思维能力优秀的学生的概率.
分析 (1)根据古典概型的概率列方程解出n,再根据人数之和为20得出m;
(2)使用组合数公式计算基本事件,利用古典概型的概率计算公式得出概率.
解答 解;(1)∵语言表达能力优秀或逻辑思维能力优秀的学生共有1+3+n+1+1=6+n,
抽到语言表达能力优秀或逻辑思维能力优秀的学生的概率为$\frac{2}{5}$.
∴$\frac{6+n}{20}=\frac{2}{5}$,解得n=2.
∴m=4.
(2)语言表达能力良好的学生共有2+4+3=9人.其中思维能力优秀的有3人,
则从9人中抽取2人共有${C}_{9}^{2}$=36个基本事件,而至少有一名思维能力优秀的基本事件个数为${C}_{3}^{2}$+${C}_{3}^{1}$•${C}_{6}^{1}$=21.
∴至少有一名逻辑思维能力优秀的学生的概率P=$\frac{21}{36}$=$\frac{7}{12}$.
点评 本题考查了古典概型的概率计算,属于基础题.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
8.执行如图的程序框图,若程序运行中输出的一组数是(x,-12),则x的值为( )


| A. | 27 | B. | 81 | C. | 243 | D. | 729 |
12.执行如图所示的程序框图,若依次输入m=${0.6^{\frac{1}{2}}}$,n=0.6-2,p=${({\frac{1}{3}})^{\frac{1}{2}}}$,则输出的结果为( )
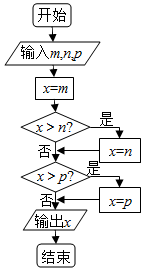

| A. | ${({\frac{1}{3}})^{\frac{1}{2}}}$ | B. | ${0.6^{\frac{1}{2}}}$ | C. | 0.6-2 | D. | ${0.6^{-\frac{3}{2}}}$ |
8.“c<0”是“方程x2+bx+c=0有根”的( )
| A. | 充要条件 | B. | 必要不充分条件 | ||
| C. | 充分不必要条件 | D. | 既不充分也不必要条件 |
 某部门就“按现有的物价水平,抚养一个孩子要花多少钱”对100人进行了问卷调查,将调查结果制作成频率分布直方图如图,已知样本中数据在区间[30,35)上的人数与数据在区间[45,50)的人数之比为3:4.
某部门就“按现有的物价水平,抚养一个孩子要花多少钱”对100人进行了问卷调查,将调查结果制作成频率分布直方图如图,已知样本中数据在区间[30,35)上的人数与数据在区间[45,50)的人数之比为3:4.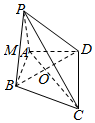 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB⊥BC,AD⊥CD,PA=AD,△BCD是边长为$\sqrt{3}$的正三角形,AC与BD交于点O,点M是PB的中点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB⊥BC,AD⊥CD,PA=AD,△BCD是边长为$\sqrt{3}$的正三角形,AC与BD交于点O,点M是PB的中点. 如图,AB是半圆O的直径,C是半圆O上除了A、B外的一个动点,DC垂直于半圆O所在的平面,DC∥EB,DC=BE,AB=4,tan∠EAB=$\frac{1}{4}$
如图,AB是半圆O的直径,C是半圆O上除了A、B外的一个动点,DC垂直于半圆O所在的平面,DC∥EB,DC=BE,AB=4,tan∠EAB=$\frac{1}{4}$