题目内容
10.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点与抛物线y2=2px(p>0)的焦点重合,若抛物线的准线交双曲线于A、B两点,当|AB|=4a时,此双曲线的离心率为( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
分析 由题意,抛物线的准线方程为x=-c,代入$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1,可得y=±$\frac{{b}^{2}}{a}$,利用|AB|=4a,求出a,b,c的关系,利用离心率公式即可得出结论.
解答 解:由题意,抛物线的准线方程为x=-c,代入$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1,可得y=±$\frac{{b}^{2}}{a}$,
∵|AB|=4a,
∴$\frac{2{b}^{2}}{a}$=4a,
∴b=$\sqrt{2}$a,
∴c=$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{3}$a,
∴e=$\frac{c}{a}$=$\sqrt{3}$.
故选:B.
点评 本题考查抛物线、双曲线的性质,考查学生的计算能力,比较基础.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
18.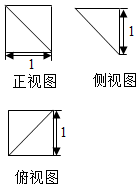 一个四棱锥的三视图如图所示,则该四棱锥的体积为( )
一个四棱锥的三视图如图所示,则该四棱锥的体积为( )
 一个四棱锥的三视图如图所示,则该四棱锥的体积为( )
一个四棱锥的三视图如图所示,则该四棱锥的体积为( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
2.M为双曲线C:$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)右支上一点,A、F分别为双曲线的左顶点和右焦点,且△MAF为等边三角形,则双曲线C的离心率为( )
| A. | $\sqrt{5}$-1 | B. | 2 | C. | 4 | D. | 6 |
18.已知点P在△ABC内(不含边界),且$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$,则$\frac{y+1}{x+2}$的取值范围为( )
| A. | ($\frac{1}{3}$,1) | B. | ($\frac{1}{2}$,1) | C. | ($\frac{2}{3}$,1) | D. | ($\frac{1}{2}$,$\frac{2}{3}$) |
 如图,三棱锥O-ABC的三条棱OA,OB,OC两两垂直且OA=OB=OC=$\sqrt{2}$,△ABC为
如图,三棱锥O-ABC的三条棱OA,OB,OC两两垂直且OA=OB=OC=$\sqrt{2}$,△ABC为 如图,AB是半圆O的直径,C是半圆O上除了A、B外的一个动点,DC垂直于半圆O所在的平面,DC∥EB,DC=BE,AB=4,tan∠EAB=$\frac{1}{4}$
如图,AB是半圆O的直径,C是半圆O上除了A、B外的一个动点,DC垂直于半圆O所在的平面,DC∥EB,DC=BE,AB=4,tan∠EAB=$\frac{1}{4}$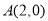 的直线
的直线 与
与 轴交于点
轴交于点 ,
,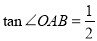 ,直线
,直线 位于
位于 轴左侧,且到
轴左侧,且到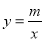 的图象经过点
的图象经过点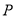 ,求
,求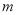 的值.
的值.