题目内容
17.已知k∈Z,$\overrightarrow{AB}$=(k,1),$\overrightarrow{BC}$=(k-2,-3),若|$\overrightarrow{AB}$|≤$\sqrt{17}$,则∠ABC是直角的概率是( )| A. | $\frac{4}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{9}$ | D. | $\frac{1}{9}$ |
分析 根据向量模长公式求出满足条件的k的个数,再根据古典概型的计算公式进行求解.
解答 解:丨$\overrightarrow{AB}$丨≤17,k∈Z,知k∈{-4,-3,-2,-1,0,1,2,3,4},
由$\overrightarrow{AB}$=(k,1),$\overrightarrow{BC}$=(k-2,-3),且垂直,k=-1,3,
∠ABC是直角的概率是$\frac{2}{9}$.
故答案选:C.
点评 本题主要考查概率的计算,根据古典概型的概率公式,利用列举法进行求解是解决本题的关键.

练习册系列答案
相关题目
8.执行如图的程序框图,若程序运行中输出的一组数是(x,-12),则x的值为( )


| A. | 27 | B. | 81 | C. | 243 | D. | 729 |
12.命题p:?x∈N,x3<x2;命题q:?a∈(0,1),函数f(x)=logax在其定义域内单调递减,则真命题是( )
| A. | ¬q | B. | p∧q | C. | ¬p∧q | D. | p∧(¬q) |

 如图,三棱锥O-ABC的三条棱OA,OB,OC两两垂直且OA=OB=OC=$\sqrt{2}$,△ABC为
如图,三棱锥O-ABC的三条棱OA,OB,OC两两垂直且OA=OB=OC=$\sqrt{2}$,△ABC为 某部门就“按现有的物价水平,抚养一个孩子要花多少钱”对100人进行了问卷调查,将调查结果制作成频率分布直方图如图,已知样本中数据在区间[30,35)上的人数与数据在区间[45,50)的人数之比为3:4.
某部门就“按现有的物价水平,抚养一个孩子要花多少钱”对100人进行了问卷调查,将调查结果制作成频率分布直方图如图,已知样本中数据在区间[30,35)上的人数与数据在区间[45,50)的人数之比为3:4.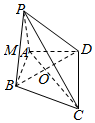 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB⊥BC,AD⊥CD,PA=AD,△BCD是边长为$\sqrt{3}$的正三角形,AC与BD交于点O,点M是PB的中点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB⊥BC,AD⊥CD,PA=AD,△BCD是边长为$\sqrt{3}$的正三角形,AC与BD交于点O,点M是PB的中点.