题目内容
20.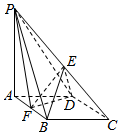 如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,AB=2,PA=3,PA⊥平面ABCD,E是PC的中点,F是AB的中点.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,AB=2,PA=3,PA⊥平面ABCD,E是PC的中点,F是AB的中点.(Ⅰ)求证:BE∥平面PDF;
(Ⅱ)求三棱锥P-DEF的体积.
分析 (I)取PD的中点为M,连结ME,MF,则可证四边形BEMF是平行四边形,得出BE∥MF,从而证明结论;
(II)VP-DEF=VC-DEF=VE-CDF=$\frac{1}{3}{S}_{△CDF}•\frac{1}{2}PA$.
解答 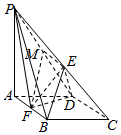 证明:(I)取PD的中点为M,连结ME,MF,
证明:(I)取PD的中点为M,连结ME,MF,
∵E是PC的中点,∴EM$\stackrel{∥}{=}$$\frac{1}{2}$CD.
又F是AB的中点,且ABCD是菱形,
∴BF$\stackrel{∥}{=}$$\frac{1}{2}$CD.
∴BF$\stackrel{∥}{=}$ME.
∴四边形MEBF是平行四边形,
∴BE∥MF.
又BE?平面PDF,MF?平面PDF
∴BE∥平面PDF.
(II)E是PC的中点
点P到平面EFD的距离与点C到平面EFD的距离相等,
故VP-DEF=VC-DEF=VE-CDF,
又S△CDF=$\frac{1}{2}{S}_{菱形ABCD}$=$\frac{1}{2}×2×2×sin60°$=$\sqrt{3}$,E到平面DFC的距离$h=\frac{1}{2}PA=\frac{3}{2}$,
∴VP-DEF=VE-CDF=$\frac{1}{3}{S}_{△CDF}•h$=$\frac{1}{3}×\sqrt{3}×\frac{3}{2}$=$\frac{{\sqrt{3}}}{2}$.
点评 本题考查了线面平行的判定,棱锥的体积计算,将棱锥进行适当转化找到与之体积相等的棱锥是关键.

练习册系列答案
相关题目
12.命题p:?x∈N,x3<x2;命题q:?a∈(0,1),函数f(x)=logax在其定义域内单调递减,则真命题是( )
| A. | ¬q | B. | p∧q | C. | ¬p∧q | D. | p∧(¬q) |
12.执行如图所示的程序框图,若依次输入m=${0.6^{\frac{1}{2}}}$,n=0.6-2,p=${({\frac{1}{3}})^{\frac{1}{2}}}$,则输出的结果为( )
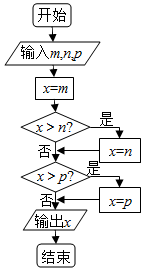

| A. | ${({\frac{1}{3}})^{\frac{1}{2}}}$ | B. | ${0.6^{\frac{1}{2}}}$ | C. | 0.6-2 | D. | ${0.6^{-\frac{3}{2}}}$ |
8.“c<0”是“方程x2+bx+c=0有根”的( )
| A. | 充要条件 | B. | 必要不充分条件 | ||
| C. | 充分不必要条件 | D. | 既不充分也不必要条件 |