题目内容
14.已知p:a>4,q:方程$\frac{{x}^{2}}{4-a}$-$\frac{{y}^{2}}{1-a}$=1表示双曲线,则p是q的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 首先求出命题q为真时,参数a的范围,再根据充要条件的定义,即可求得答案.
解答 解:命题q:方程$\frac{{x}^{2}}{4-a}$-$\frac{{y}^{2}}{1-a}$=1表示双曲线1表示双曲线?(4-a)(1-a)>0?a>4或a<1.
由于命题p:a>4⇒命题q:a<-1或a>0;反之不能.
则p是q的充分不必要条件.
故选A
点评 本题考查双曲线的方程,考查了命题的真假与应用,是一个中档题目.

练习册系列答案
相关题目
2.在△ABC中,角A、B、C的对边分别为a、b、c,且满足(b-a)sinA=(b-c)(sinB+sinC),则角C等于( )
| A. | $\frac{π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{2π}{3}$ |
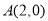 的直线
的直线 与
与 轴交于点
轴交于点 ,
,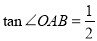 ,直线
,直线 位于
位于 轴左侧,且到
轴左侧,且到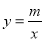 的图象经过点
的图象经过点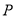 ,求
,求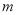 的值.
的值.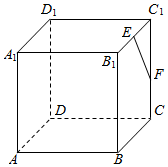 如图所示,在正方体ABCD-A1B1C1D1中,E、F分别是B1C1,CC1的中点.求:
如图所示,在正方体ABCD-A1B1C1D1中,E、F分别是B1C1,CC1的中点.求: