题目内容
14.已知双曲线$\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1的左右焦点分别为F1、F2,点P为双曲线上一点,△F1PF2的内切圆圆心为M,若S${\;}_{△{F}_{1}PM}$=S${\;}_{△{F}_{2}PM}$+8,那么S${\;}_{△{F}_{1}M{F}_{2}}$( )| A. | 2$\sqrt{7}$ | B. | 6 | C. | 8 | D. | 10 |
分析 求得双曲线的a,b,c,设△F1PF2的内切圆的半径为r,运用三角形的面积公式,结合双曲线的定义,求得r=2,再由三角形的面积公式计算即可得到所求值.
解答 解:双曲线$\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{9}$=1的a=4,b=3,可得c=$\sqrt{{a}^{2}+{b}^{2}}$=5,
设△F1PF2的内切圆的半径为r,
由S${\;}_{△{F}_{1}PM}$=S${\;}_{△{F}_{2}PM}$+8,
可得$\frac{1}{2}$r|PF1|=$\frac{1}{2}$r|PF2|+8,
由双曲线的定义可得|PF1|-|PF2|=2a=8,
可得$\frac{1}{2}$r(|PF1|-|PF2|)=8,
即有4r=8,解得r=2,
则S${\;}_{△{F}_{1}M{F}_{2}}$=$\frac{1}{2}$r|F1F2|=2c=10.
故选:D.
点评 本题考查双曲线的定义和方程的运用,注意运用定义法解题,同时考查三角形的面积公式的运用,考查运算能力,属于基础题.

练习册系列答案
相关题目
2.M为双曲线C:$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)右支上一点,A、F分别为双曲线的左顶点和右焦点,且△MAF为等边三角形,则双曲线C的离心率为( )
| A. | $\sqrt{5}$-1 | B. | 2 | C. | 4 | D. | 6 |
18.已知点P在△ABC内(不含边界),且$\overrightarrow{AP}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$,则$\frac{y+1}{x+2}$的取值范围为( )
| A. | ($\frac{1}{3}$,1) | B. | ($\frac{1}{2}$,1) | C. | ($\frac{2}{3}$,1) | D. | ($\frac{1}{2}$,$\frac{2}{3}$) |
2.在△ABC中,角A、B、C的对边分别为a、b、c,且满足(b-a)sinA=(b-c)(sinB+sinC),则角C等于( )
| A. | $\frac{π}{3}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{2π}{3}$ |
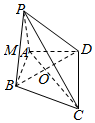 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB⊥BC,AD⊥CD,PA=AD,△BCD是边长为$\sqrt{3}$的正三角形,AC与BD交于点O,点M是PB的中点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB⊥BC,AD⊥CD,PA=AD,△BCD是边长为$\sqrt{3}$的正三角形,AC与BD交于点O,点M是PB的中点.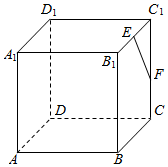 如图所示,在正方体ABCD-A1B1C1D1中,E、F分别是B1C1,CC1的中点.求:
如图所示,在正方体ABCD-A1B1C1D1中,E、F分别是B1C1,CC1的中点.求: