题目内容
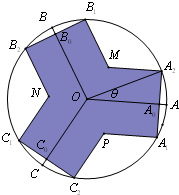 如图,半径为1的圆O,∠AOB=∠BOC=∠COA=
如图,半径为1的圆O,∠AOB=∠BOC=∠COA=| 2π |
| 3 |
(1)设θ∈(0,
| π |
| 3 |
(2)在(1)的条件下,求y=f(θ)的最大值,并求出当函数取最大值是时tan2θ的值.
考点:在实际问题中建立三角函数模型
专题:综合题,三角函数的求值
分析:(1)由题意,y=6SOA0A2M,四边形OA0A2M为直角梯形,即可求y=f(θ)的解析式;
(2)f(θ)=
sin(2θ+φ)-
(tanφ=
),即可求出y=f(θ)的最大值,同时可得当函数取最大值是时tan2θ的值.
(2)f(θ)=
| ||
| 2 |
| ||
| 2 |
| 1 | ||
2
|
解答:
解:(1)由题意,y=6SOA0A2M,
A0A2=OA2sinθ=sinθ,OA0=cosθ,
由图可知,四边形OA0A2M为直角梯形,
∴6SOA0A2M=
(MA2+OA0)•A0A2
由图知,M,N,P对称,∴∠MOP=120°,
∴∠MOH=60°,
∴在Rt△OMH中,OH=
=
,
∴SOA0A2M=
[(cosθ-
)+cosθ]sinθ=
sin2θ-
,
∴y=3sin2θ+
cos2θ-
(θ∈(0,
]),
(2)f(θ)=
sin(2θ+φ)-
(tanφ=
)
∵θ∈(0,
],tanφ=
<
,
∴φ∈(0,
)
∴2θ+φ=
时,y=f(θ)的最大值为
,
此时2θ=
-φ,tan2θ=tan(
-φ)=
=2
.
A0A2=OA2sinθ=sinθ,OA0=cosθ,
由图可知,四边形OA0A2M为直角梯形,
∴6SOA0A2M=
| 1 |
| 2 |
由图知,M,N,P对称,∴∠MOP=120°,
∴∠MOH=60°,
∴在Rt△OMH中,OH=
| MH | ||
|
| sinθ | ||
|
∴SOA0A2M=
| 1 |
| 2 |
| sinθ | ||
|
| 1 |
| 2 |
| sin2θ | ||
2
|
∴y=3sin2θ+
| ||
| 2 |
| ||
| 2 |
| π |
| 3 |
(2)f(θ)=
| ||
| 2 |
| ||
| 2 |
| 1 | ||
2
|
∵θ∈(0,
| π |
| 3 |
| 1 | ||
2
|
| 1 | ||
|
∴φ∈(0,
| π |
| 6 |
∴2θ+φ=
| π |
| 2 |
| ||||
| 2 |
此时2θ=
| π |
| 2 |
| π |
| 2 |
| 1 |
| tanθ |
| 3 |
点评:本题考查利用数学知识解决实际问题,考查是三角函数知识的运用,正确确定函数解析式是关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
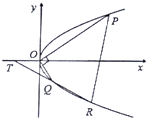 如图,已知抛物线y2=x,过原点O作两条相互垂直的直线,分别交抛物线于点P,Q
如图,已知抛物线y2=x,过原点O作两条相互垂直的直线,分别交抛物线于点P,Q