题目内容
已知数列an的首项a1=2,且an=2an-1-1(n?N+,n≥2).
(1)求数列{an}的通项公式;
(2)求数列{nan-n}的前n项和Sn.
(1)求数列{an}的通项公式;
(2)求数列{nan-n}的前n项和Sn.
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(1)根据条件构造一个等比数列,即可求数列{an}的通项公式;
(2)求出数列{nan-n}的通项公式,利用错位相减法即可求出前n项和Sn.
(2)求出数列{nan-n}的通项公式,利用错位相减法即可求出前n项和Sn.
解答:
解:(1)∵an=2an-1-1,
∴an-1=2(an-1-1),
即{an-1}是以a1-1=2-1=1,为首项,公比q=2的等比数列,
∴an-1=2n-1,即an=1+2n-1.;
(2)∵an=1+2n-1.,
∴nan-n=n(1+2n-1)-n=n•2n-1,
数列{nan-n}的前n项和Sn=1•20+2•21+3•22+…+n•2n-1,①
2Sn=1•21+2•22+3•23+…+(n-1)•2n-1+n•2n,②,
①-②得,-Sn=1•20+21+22+…+2n-1-n•2n=
-n•2n=2n-n•2n-1=(1-n)•2n-1,
即Sn=(n+1)•2n+1.
∴an-1=2(an-1-1),
即{an-1}是以a1-1=2-1=1,为首项,公比q=2的等比数列,
∴an-1=2n-1,即an=1+2n-1.;
(2)∵an=1+2n-1.,
∴nan-n=n(1+2n-1)-n=n•2n-1,
数列{nan-n}的前n项和Sn=1•20+2•21+3•22+…+n•2n-1,①
2Sn=1•21+2•22+3•23+…+(n-1)•2n-1+n•2n,②,
①-②得,-Sn=1•20+21+22+…+2n-1-n•2n=
| 1-2n |
| 1-2 |
即Sn=(n+1)•2n+1.
点评:本题主要考查数列的通项公式以及数列求和问题,利用构造法构造一个等比数列是解决本题的关键,要求熟练掌握错位相减法求和.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
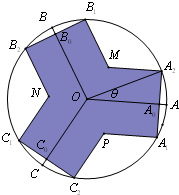 如图,半径为1的圆O,∠AOB=∠BOC=∠COA=
如图,半径为1的圆O,∠AOB=∠BOC=∠COA=