题目内容
已知数列{an}是以公比为q的等比数列,Sn(n∈N*)是其前n项和,且S3,S9,S6成等差数列.
(1)求证:a2,a8,a5也成等差数列;
(2)判断以a2,a8,a5为前三项的等差数列的第四项是否也是数列{an}中的项?若是,求出这一项;若不是,请说明理由.
(1)求证:a2,a8,a5也成等差数列;
(2)判断以a2,a8,a5为前三项的等差数列的第四项是否也是数列{an}中的项?若是,求出这一项;若不是,请说明理由.
考点:等差数列与等比数列的综合
专题:等差数列与等比数列
分析:首先将给出的项、和都用等比数列的首项、公比表示出来,然后进行化简,然后利用等差数列的定义构造等量关系和证明要证的结论;第二问是一个探究性问题,一般先假设结论成立,然后以此为条件结合已知条件进行推导,若推导出结果成立则结论成立,若推出矛盾,则结论不成立.
解答:
解:(Ⅰ)证明:当q=1时,S3=3a1,S9=9a1,S6=6a1,而a1≠0,
∴S3,S9,S6不可能是等差数列,故q≠1.
当q≠1时,∵S3,S9,S6成等差数列,
∴2S9=S3+S6,又Sn=
,
∴2
=
+
,
化简得2q7=q+q4,所以2a1q7=a1q+a1q4,
∴2a8=a2+a5,故a2、a8、a5成等差数列.
(Ⅱ)由2q6=1+q3得q3=1(舍)或q3=-
,
要使以a2,a8,a5为前三项的等差数列的第四项是数列{an}中的项且为第k项,
则必有ak-a5=a5-a8,即2a5=a8+ak,
两边同除以a2,得2q3=qk-2+q6,
将q3=-
代入,解得qk-2=-
,
又∵(q3)k-2=(-
)k-2,即(qk-2)3=(-
)k-2,
∴(-
)k-2=(-
)3,
由于k是正整数,所以(-
)k-2=(-
)3不可能成立,
∴以a2,a8,a5为前三项的等差数列的第四项不可能是数列{an}中的项.
∴S3,S9,S6不可能是等差数列,故q≠1.
当q≠1时,∵S3,S9,S6成等差数列,
∴2S9=S3+S6,又Sn=
| a1(1-qn) |
| 1-q |
∴2
| a1(1-q9) |
| 1-q |
| a1(1-q3) |
| 1-q |
| a1(1-q6) |
| 1-q |
化简得2q7=q+q4,所以2a1q7=a1q+a1q4,
∴2a8=a2+a5,故a2、a8、a5成等差数列.
(Ⅱ)由2q6=1+q3得q3=1(舍)或q3=-
| 1 |
| 2 |
要使以a2,a8,a5为前三项的等差数列的第四项是数列{an}中的项且为第k项,
则必有ak-a5=a5-a8,即2a5=a8+ak,
两边同除以a2,得2q3=qk-2+q6,
将q3=-
| 1 |
| 2 |
| 5 |
| 4 |
又∵(q3)k-2=(-
| 1 |
| 2 |
| 1 |
| 2 |
∴(-
| 1 |
| 2 |
| 5 |
| 4 |
由于k是正整数,所以(-
| 1 |
| 2 |
| 5 |
| 4 |
∴以a2,a8,a5为前三项的等差数列的第四项不可能是数列{an}中的项.
点评:对于等差、等比数列问题,一般是用基本量首项、公差(比)借助通项公式、求和公式把已知条件和结论表示出来,然后进行化简,再寻找条件与结论之间的关系进行推理、证明与计算,要注意定义、性质的应用;探究性问题一般是先假设结论成立,构造方程或不等式,只要是有符合的解,则结论成立,否则不成立.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
复数z=
,|
|是( )
| 5 |
| 3+4i |
. |
| z |
| A、25 | B、5 | C、1 | D、7 |
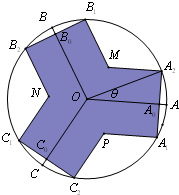 如图,半径为1的圆O,∠AOB=∠BOC=∠COA=
如图,半径为1的圆O,∠AOB=∠BOC=∠COA=