题目内容
若各项为正数的数列{an）的前n项和为Sn，首项a1=1，a2=3，点P（
，Sn+2）（n∈N+）在函数y=（x+1）2的图象上
（1）求a3；
（2）求数列{an）的通项公式；
（3）设数列{cn）的通项公式为cn=
，是否存在整数t，使得数列{cn）中存在项ck（k≥3，k∈N+），满足c1，c2，ck：构成等差数列，若存在，请求出所有符合条件的t的值；若不存在，请说明理由．
| Sn+1 |
（1）求a3；
（2）求数列{an）的通项公式；
（3）设数列{cn）的通项公式为cn=
| an |
| an+t |
考点：数列与不等式的综合
专题：等差数列与等比数列
分析：（1）由已知条件得Sn+2=(
+1)2，令n=1，则a1+a2+a3=(
+1)2，由此能求出a3．
（2）由Sn+2=(
+1)2，得
-
=1，从而得到数列{
}是以
为首项，1为公差的等差数列，由此能求出数列{an）的通项公式．
（3）cn=
，要使c1，c2，ck成等差数列，必须
=
+
，由此能求出所有符合条件的t值．
| Sn+1 |
| a1+a2 |
（2）由Sn+2=(
| Sn+1 |
| Sn+2 |
| Sn+1 |
| Sn |
| S1 |
（3）cn=
| 2n-1 |
| 2n-1+t |
| 6 |
| 3+t |
| 1 |
| 1+t |
| 2k-1 |
| 2k-1+t |
解答：
解：（1）∵点P（
，Sn+2）（n∈N+）在函数y=（x+1）2的图象上，
∴Sn+2=(
+1)2，…（1分）
令n=1，则S3=（
+1）2，…（2分）
即a1+a2+a3=(
+1)2，
∴a3=(
+1)2-a1-a2=（
+1)2-1-3=52-1-3=5．…（3分）
（2）由Sn+2=(
+1)2，得
-
=1．…（4分）
又
-
=
-
=1，…（5分）
∴数列{
}是以
为首项，1为公差的等差数列，
∴
=
+(n-1)×1，即Sn=n2，…（6分）
当n≥2时，an=Sn-Sn-1
=n2-（n-1）2
=2n-1，…（8分）
∵a1=1也满足上式，
∴an=2n-1．…（9分）
（3）由（2）知，cn=
=
，
要使c1，c2，ck成等差数列，必须2c2=c1+ck，
即
=
+
，…（10分）
化简得k=3+
．…（12分）
∵k≥3，k∈N*，且t为整数，∴t-1只能为1，2，4，…（13分）
∴所有符合条件的t值为2，3，5．…（14分）
| Sn+1 |
∴Sn+2=(
| Sn+1 |
令n=1，则S3=（
| S2 |
即a1+a2+a3=(
| a1+a2 |
∴a3=(
| a1+a2 |
| 1+3 |
（2）由Sn+2=(
| Sn+1 |
| Sn+2 |
| Sn+1 |
又
| S2 |
| S1 |
| a1+a2 |
| a1 |
∴数列{
| Sn |
| S1 |
∴
| Sn |
| S1 |
当n≥2时，an=Sn-Sn-1
=n2-（n-1）2
=2n-1，…（8分）
∵a1=1也满足上式，
∴an=2n-1．…（9分）
（3）由（2）知，cn=
| an |
| an+t |
| 2n-1 |
| 2n-1+t |
要使c1，c2，ck成等差数列，必须2c2=c1+ck，
即
| 6 |
| 3+t |
| 1 |
| 1+t |
| 2k-1 |
| 2k-1+t |
化简得k=3+
| 4 |
| t-1 |
∵k≥3，k∈N*，且t为整数，∴t-1只能为1，2，4，…（13分）
∴所有符合条件的t值为2，3，5．…（14分）
点评：本题考查数列的通项公式的求法，考查符合条件的实数值是否存在的判断与嫠法，解题时要认真审题，注意等差数列的性质的灵活运用．
练习册系列答案
阅读快车系列答案
相关题目
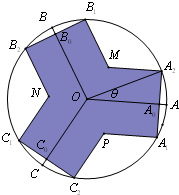如图，半径为1的圆O，∠AOB=∠BOC=∠COA=