Question

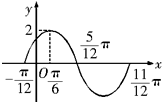函数y=Asin（ωx+ϕ）(A＞0，ω＞0，|φ|＜

π

2

)一段图象如图所示．
（1）分别求出A，ω，ϕ并确定函数的解析式；
（2）求函数f（x）的单调递增区间；
（3）并指出函数y=Asin（ωx+ϕ）的图象是由函数y=sinx的图象怎样变换得到．

Answer 1

考点：由y=Asin（ωx+φ）的部分图象确定其解析式,函数y=Asin（ωx+φ）的图象变换

专题：三角函数的图像与性质

分析：（1）根据三角函数的图象求出A，ω，ϕ，即可确定函数的解析式；
（2）根据函数的表达式，即可求函数f（x）的单调递增区间；
（3）根据三角函数的关系即可得到结论．

解答： 解：（1）由函数的图象可知A=2，T=π，
∵T=

2π

ω

=π，
∴ω=2，
∵函数的图象经过(-

π

12

，0)，
∴2sin(-

π

12

×2+ϕ)=0，
又|ϕ|＜

π

12

，
∴ϕ=

π

6

；
∴函数的解析式为：y=2sin(2x+

π

6

)．
（2）由已知得-

π

2

+2kπ≤2x+

π

6

≤

π

2

+2kπ，k∈Z，
解得-

π

3

+kπ≤x≤

π

6

+kπ，k∈Z，
∴函数的单调递增区间为[-

π

3

+kπ．
（3）将函数y=sinx的图象向左平移

π

6

个单位得到y=sin(x+

π

6

)的图象，
纵坐标不变横坐标缩小到原来的

1

2

倍得到函数y=sin(2x+

π

6

)的图象，
接下来横坐标不变纵坐标扩大到原来的2倍得到函数y=2sin(2x+

π

6

)的图象．

点评：本题主要考查三角函数解析式的求法，根据三角函数的图象是解决本题的关键，要求熟练掌握三角函数的图象和性质．