题目内容
若
=
,则tan2α=( )
| 1+cos2α |
| sin2α |
| 1 |
| 2 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
考点:同角三角函数基本关系的运用
专题:三角函数的求值
分析:已知等式分子利用同角三角函数间的基本关系变形,分子分母除以cos2α变形后,即可确定出tan2α的值.
解答:
解:∵
=
,即sin2α=2cos2α+2,sin22α+cos22α=1,
∴(2cos2α+2)2+cos22α=1,即(cos2α+1)(5cos2α+3)=0,
解得:cos2α=-1(此时sin2α=0,不合题意)或cos2α=-
,
∴sin2α=2×(-
)+2=
,
则tan2α=
=-
.
故选:D.
| 1+cos2α |
| sin2α |
| 1 |
| 2 |
∴(2cos2α+2)2+cos22α=1,即(cos2α+1)(5cos2α+3)=0,
解得:cos2α=-1(此时sin2α=0,不合题意)或cos2α=-
| 3 |
| 5 |
∴sin2α=2×(-
| 3 |
| 5 |
| 4 |
| 5 |
则tan2α=
| sin2α |
| cos2α |
| 4 |
| 3 |
故选:D.
点评:此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.

练习册系列答案
 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
已知函数f(x)=
-mx+1的图象为曲线C,若曲线C存在与直线y=
x垂直的切线,则实数m的取值范围是( )
| e | x |
| 1 |
| 2 |
| A、m≤2 | ||
| B、m>2 | ||
C、m≤
| ||
D、m>-
|
已知△ABC的顶点A(2,3),且三条中线交于点G(4,1),则BC边上的中点坐标为( )
| A、(5,0) |
| B、(6,-1) |
| C、(5,-3) |
| D、(6,-3) |
设x是实数,且满足等式
+
=cosθ,则实数θ等于(以下各式中k∈Z)( )
| x |
| 2 |
| 1 |
| 2x |
| A、2kπ | ||
| B、(2k+1)π | ||
| C、kπ | ||
D、kπ+
|
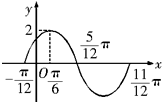 函数y=Asin(ωx+ϕ)
函数y=Asin(ωx+ϕ)