题目内容
已知命题p:log2|1-
|>1;命题q:x2-(2m+1)x+m2+m≥0,若p是¬q的必要非充分条件,求实数m的取值范围.
| x-1 |
| 3 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:先求出命题p,q的等价条件,然后利用p是¬q的必要非充分条件,建立条件关系即可求出m的取值范围.
解答:
解:∵log2|1-
|>1;
∴|1-
|>2,即x<-2或x>10,A=(-∞,-2)∪(10,+∞);
命题¬q:x2-(2m+1)x+m2+m<0,
即m<x<m+1,
即B=(m,m+1),
∵p是¬q的必要非充分条件,则B是A的真子集,
则m+1≤-2或m≥10.
即m≤-3或m≥10.
| x-1 |
| 3 |
∴|1-
| x-1 |
| 3 |
命题¬q:x2-(2m+1)x+m2+m<0,
即m<x<m+1,
即B=(m,m+1),
∵p是¬q的必要非充分条件,则B是A的真子集,
则m+1≤-2或m≥10.
即m≤-3或m≥10.
点评:本题主要考查充分条件和必要条件的应用,根据不等式的性质求出命题p,q的等价条件是解决本题的关键.

练习册系列答案
相关题目
在△ABC中,已知a2+b2=c2+
ba,则∠C=( )
| 2 |
| A、30° | B、150° |
| C、45° | D、135° |
已知f(x)是定义在R上的偶函数,对任意的x∈R,都有f(2+x)=-f(x),且当x∈[0,1]时f(x)=-x2+1,则方程f(x)=k,k∈[0,1)在[-1,5]的所有实根之和为( )
| A、0 | B、2 | C、4 | D、8 |
已知△ABC的顶点A(2,3),且三条中线交于点G(4,1),则BC边上的中点坐标为( )
| A、(5,0) |
| B、(6,-1) |
| C、(5,-3) |
| D、(6,-3) |
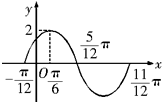 函数y=Asin(ωx+ϕ)
函数y=Asin(ωx+ϕ)