题目内容
在△ABC中,点B的坐标为(-1,0),BC边上的高所在直线的方程为x-4y+5=0,∠A的平分线所在直线的方程为x-y-1=0,求点A,C的坐标.
考点:两条直线的交点坐标
专题:直线与圆
分析:首先联立BC边上的高所在的直线和∠A的平分线所在的直线,求出A点坐标,然后点B关于∠A的平分线对称的点,从而得出AC所在直线的方程,即可得出点C的坐标.
解答:
C解:由
解得,A(3,2)
设点B关于∠A的平分线对称的点为D(m,n),则:
解得,D(1,-2)
由角分线性质知:点D在直线AC上,故直线AC的方程为:y=2x-4
设点C的坐标为(x,y),则
解得:
即C(0,-4).
|
设点B关于∠A的平分线对称的点为D(m,n),则:
|
解得,D(1,-2)
由角分线性质知:点D在直线AC上,故直线AC的方程为:y=2x-4
设点C的坐标为(x,y),则
|
|
点评:熟练掌握两条直线的交点,点关于直线的对称关系等是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知抛物线y2=2px(p>0),过其焦点且斜率为1的直线交抛物线于A,B两点,若线段AB的中点的纵坐标为2,则该抛物线的标准方程为( )
| A、y2=-4x |
| B、y2=4x |
| C、x2=4y |
| D、x2=-4y |
若过点P(6,m)和Q(m,3)的直线与斜率为
的直线垂直,则m的值为( )
| 1 |
| 2 |
| A、9 | B、4 | C、0 | D、5 |
已知f(x)是定义在R上的偶函数,对任意的x∈R,都有f(2+x)=-f(x),且当x∈[0,1]时f(x)=-x2+1,则方程f(x)=k,k∈[0,1)在[-1,5]的所有实根之和为( )
| A、0 | B、2 | C、4 | D、8 |
已知点P是抛物线y2=6x上的一个动点,则点P到点M(0,2)的距离与点P到该抛物线的准线的距离之和的最小值为( )
| A、2 | ||
| B、3 | ||
C、
| ||
D、
|
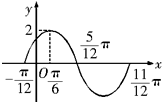 函数y=Asin(ωx+ϕ)
函数y=Asin(ωx+ϕ)