题目内容
直线Ax+By=0,若从0,1,2,3,5,7这六个数字中每次取两个不同的数作为A,B的值,则表示成不同直线的条数是( )
| A、2 | B、12 | C、22 | D、25 |
考点:直线的一般式方程
专题:直线与圆
分析:选中0时,Ax+By=0共能表达2条直线;当A、B从1,2,3,5,7五个数字中取值时,应使用组合数计算.
解答:
解:①当A或B中有一个取0时,另一个不论取何值,
方程都只能表达2条直线,即x=0和y=0.
即选中0时,Ax+By=0共能表达2条直线;
②当A、B从1,2,3,5,7五个数字中取值时,应使用组合计算
=5×4=20.
即当A、B从1,2,3,5,7五个数字中取值时,Ax+By=0共能表达20条直线.
综上所述,表示成不同直线的条数是22条.
故选C.
方程都只能表达2条直线,即x=0和y=0.
即选中0时,Ax+By=0共能表达2条直线;
②当A、B从1,2,3,5,7五个数字中取值时,应使用组合计算
| A | 2 5 |
即当A、B从1,2,3,5,7五个数字中取值时,Ax+By=0共能表达20条直线.
综上所述,表示成不同直线的条数是22条.
故选C.
点评:本题考查满足条件的直线条数的求法,解题时要注意分类讨论思想和排列组合知识的合理运用.

练习册系列答案
相关题目
已知抛物线y2=2px(p>0),过其焦点且斜率为1的直线交抛物线于A,B两点,若线段AB的中点的纵坐标为2,则该抛物线的标准方程为( )
| A、y2=-4x |
| B、y2=4x |
| C、x2=4y |
| D、x2=-4y |
抛物线2x2+y=0的焦点坐标是( )
A、(0,-
| ||
B、(0,-
| ||
C、(-
| ||
D、(-
|
在△ABC中,已知a2+b2=c2+
ba,则∠C=( )
| 2 |
| A、30° | B、150° |
| C、45° | D、135° |
若θ是任意实数,则方程x2+4y2cosθ=1所表示的曲线一定不是( )
| A、圆 | B、双曲线 | C、直线 | D、抛物线 |
若过点P(6,m)和Q(m,3)的直线与斜率为
的直线垂直,则m的值为( )
| 1 |
| 2 |
| A、9 | B、4 | C、0 | D、5 |
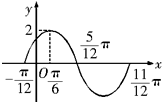 函数y=Asin(ωx+ϕ)
函数y=Asin(ωx+ϕ)