题目内容
(1)用辗转相除法求出372和684的最大公约数,然后用更相减损术验证.
(2)用秦九韶算法求多项式f(x)=x6-12x5+60x4-160x3+240x2-192x+64当x=2时的值.
(2)用秦九韶算法求多项式f(x)=x6-12x5+60x4-160x3+240x2-192x+64当x=2时的值.
考点:秦九韶算法,排序问题与算法的多样性
专题:计算题,算法和程序框图
分析:(1)用较大的数字除以较小的数字,得到商和余数,然后再用上一式中的除数和得到的余数中较大的除以较小的,以此类推,当整除时,就得到要求的最大公约数;更相减损术:用较大的数字减去较小的数字,得到差,仍用差和减数中较大的数字减去较小的数字,这样依次做下去,等做到减数和差相等时,得到结果.
(2)将f(x)改写为f(x)=(((((x-12)x+60)x-160)x+240)x-192)x+64,由内向外依次计算一次多项式当x=2时的值,即可得出结论.
(2)将f(x)改写为f(x)=(((((x-12)x+60)x-160)x+240)x-192)x+64,由内向外依次计算一次多项式当x=2时的值,即可得出结论.
解答:
解:(1)∵684=1×372+312
372=1×312+60
312=5×60+12
60=5×12
∴(372,684)=12
检验:684-372=312
372-312=60
312-60=252
252-60=192
192-60=132
132-60=72
72-60=12
60-12=48
48-12=36
36-12=24
24-12=12
经检验:(372,684)=12;
(2)将f(x)改写为f(x)=(((((x-12)x+60)x-160)x+240)x-192)x+64
由内向外依次计算一次多项式当x=2时的值,
v0=1,
v1=1×2-12=-10,
v2=-10×2+60=40,
v3=40×2-160=-80,
v4=-80×2+240=80,
v5=80×2-192=-32,
v6=-32×2+64=0.
∴f(2)=0,即x=2时,原多项式的值为0.
372=1×312+60
312=5×60+12
60=5×12
∴(372,684)=12
检验:684-372=312
372-312=60
312-60=252
252-60=192
192-60=132
132-60=72
72-60=12
60-12=48
48-12=36
36-12=24
24-12=12
经检验:(372,684)=12;
(2)将f(x)改写为f(x)=(((((x-12)x+60)x-160)x+240)x-192)x+64
由内向外依次计算一次多项式当x=2时的值,
v0=1,
v1=1×2-12=-10,
v2=-10×2+60=40,
v3=40×2-160=-80,
v4=-80×2+240=80,
v5=80×2-192=-32,
v6=-32×2+64=0.
∴f(2)=0,即x=2时,原多项式的值为0.
点评:本题考查的知识点是辗转相除法和更相减损术,考查秦九韶算法,熟练掌握辗转相除法和更相减损术求最大公约数的方法和步骤是解答本题的关键.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
若θ是任意实数,则方程x2+4y2cosθ=1所表示的曲线一定不是( )
| A、圆 | B、双曲线 | C、直线 | D、抛物线 |
已知点P是抛物线y2=6x上的一个动点,则点P到点M(0,2)的距离与点P到该抛物线的准线的距离之和的最小值为( )
| A、2 | ||
| B、3 | ||
C、
| ||
D、
|
设x是实数,且满足等式
+
=cosθ,则实数θ等于(以下各式中k∈Z)( )
| x |
| 2 |
| 1 |
| 2x |
| A、2kπ | ||
| B、(2k+1)π | ||
| C、kπ | ||
D、kπ+
|
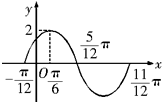 函数y=Asin(ωx+ϕ)
函数y=Asin(ωx+ϕ)