题目内容
△ABC中,角A,B,C的对边分别为a,b,c.若a,b,c成等比数列,且sinC=2sinA.则cosB=( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:余弦定理
专题:解三角形
分析:由题设条件得,b2=ac,再由正弦定理与sinA=2sinC,可解得a=2c,将这些代入由余弦定理得出的关于cosB的方程即可求出结果.
解答:
解:∵在△ABC中,a,b,c成等比数列,且sinC=2sinA,
∴b2=ac,由正弦定理得a=2c,
由余弦定理得b2=a2+c2-2accosB,
将b2=ac及a=2c代入上式解得cosB=
,
故选:B.
∴b2=ac,由正弦定理得a=2c,
由余弦定理得b2=a2+c2-2accosB,
将b2=ac及a=2c代入上式解得cosB=
| 3 |
| 4 |
故选:B.
点评:考查正弦定理与余弦定理,属于运用定理建立所求量的方程通过解方程来求值的题目,训练目标是灵活运用公式求值,属于中档题.

练习册系列答案
相关题目
若θ是任意实数,则方程x2+4y2cosθ=1所表示的曲线一定不是( )
| A、圆 | B、双曲线 | C、直线 | D、抛物线 |
若过点P(6,m)和Q(m,3)的直线与斜率为
的直线垂直,则m的值为( )
| 1 |
| 2 |
| A、9 | B、4 | C、0 | D、5 |
《几何原本》的作者是( )
| A、欧几里得 | B、阿基米德 |
| C、阿波罗尼奥斯 | D、托勒玫 |
已知f(x)是定义在R上的偶函数,对任意的x∈R,都有f(2+x)=-f(x),且当x∈[0,1]时f(x)=-x2+1,则方程f(x)=k,k∈[0,1)在[-1,5]的所有实根之和为( )
| A、0 | B、2 | C、4 | D、8 |
已知点P是抛物线y2=6x上的一个动点,则点P到点M(0,2)的距离与点P到该抛物线的准线的距离之和的最小值为( )
| A、2 | ||
| B、3 | ||
C、
| ||
D、
|
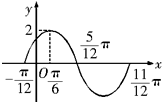 函数y=Asin(ωx+ϕ)
函数y=Asin(ωx+ϕ)