题目内容
已知函数f(x)=(x2+ax+3)ex(x∈R)在x=2处的切线的斜率为2e2.
(1)求函数f(x)的解析式并求单调区间;
(2)设g(x)=
,其中x∈[-2,m),问:对于任意的m>-2,方程g(x)=
(m-1)2在区间(-2,m)上是否存在实数根?若存在,请确定实数根的个数.若不存在,请说明理由.
(1)求函数f(x)的解析式并求单调区间;
(2)设g(x)=
| f′(x) |
| ex |
| 2 |
| 3 |
考点:利用导数研究曲线上某点切线方程,利用导数研究函数的单调性,函数在某点取得极值的条件
专题:综合题,导数的综合应用
分析:(1)求导函数,利用函数f(x)=(x2+ax+3)ex(x∈R)在x=2处的切线的斜率为2e2,求出a的值,利用导数的正负,可得函数的单调区间;
(2)假设方程g(x)=
(m-1)2在区间(-2,m)上存在实数根.设x0是方程g(x)=
(m-1)2的实根,x02-x0=
(m-1)2,令h(x)=x2-x-
(m-1)2,从而问题转化为证明方程h(x)=x2-x-
(m-1)2=0在(-2,m)上有实根,并讨论解的个数.
(2)假设方程g(x)=
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
解答:
解:(1)由已知得f'(x)=[x2+(a+2)x+(a+3)]ex…(1分)
所以f'(2)=2e2=(11+3a)e2
故a=-3,即f(x)=(x2-3x+3)ex. …(3分)
由f′(x)=(x2-x)ex>0得x<0或x>1;
由f′(x)<0,可得0<x<1.
故f(x)单调增区间是(-∞,0),(1,+∞),单调减区间是(0,1)…(5分).
(2)假设方程g(x)=
(m-1)2在区间(-2,m)上存在实数根
设x0是方程g(x)=
(m-1)2的实根,x02-x0=
(m-1)2,
令h(x)=x2-x-
(m-1)2,从而问题转化为证明方程h(x)=x2-x-
(m-1)2=0在(-2,m)上有实根,并讨论解的个数…(7分)
因为h(-2)=6-
(m-1)2=-
(m+2)(m-4),h(m)=m(m-1)-
(m-1)2=
(m+2)(m-1),
所以
①当m>4或-2<m<1时,h(-2)h(m)<0,所以h(x)=0在(-2,m)上有解,且只有一解
②当1<m<4时,h(-2)>0且h(m)>0,但由于h(0)=-
(m-1)2<0,
所以h(x)=0在(-2,m)上有解,且有两解 …(10分)
③当m=1时,h(x)=x2-x=0,所以x=0或x=1,所以h(x)=0在(-2,m)上有且只有一解;
当m=4时,h(x)=x2-x-6=0,所以x=-2或x=3,
所以h(x)=0在(-2,4)上也有且只有一解…(12分)
综上所述,对于任意的m>-2,方程g(x)=
(m-1)2在区间(-2,m)上均有实数根
且当m≥4或-2<m≤1时,有唯一的实数解;当1<m<4时,有两个实数解…(14分)
所以f'(2)=2e2=(11+3a)e2
故a=-3,即f(x)=(x2-3x+3)ex. …(3分)
由f′(x)=(x2-x)ex>0得x<0或x>1;
由f′(x)<0,可得0<x<1.
故f(x)单调增区间是(-∞,0),(1,+∞),单调减区间是(0,1)…(5分).
(2)假设方程g(x)=
| 2 |
| 3 |
设x0是方程g(x)=
| 2 |
| 3 |
| 2 |
| 3 |
令h(x)=x2-x-
| 2 |
| 3 |
| 2 |
| 3 |
因为h(-2)=6-
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
所以
①当m>4或-2<m<1时,h(-2)h(m)<0,所以h(x)=0在(-2,m)上有解,且只有一解
②当1<m<4时,h(-2)>0且h(m)>0,但由于h(0)=-
| 2 |
| 3 |
所以h(x)=0在(-2,m)上有解,且有两解 …(10分)
③当m=1时,h(x)=x2-x=0,所以x=0或x=1,所以h(x)=0在(-2,m)上有且只有一解;
当m=4时,h(x)=x2-x-6=0,所以x=-2或x=3,
所以h(x)=0在(-2,4)上也有且只有一解…(12分)
综上所述,对于任意的m>-2,方程g(x)=
| 2 |
| 3 |
且当m≥4或-2<m≤1时,有唯一的实数解;当1<m<4时,有两个实数解…(14分)
点评:本题考查导数知识的运用,考查导数的几何意义,考查函数的单调性,考查分类讨论的数学思想,考查学生分析转化问题的能力,正确分类是关键.

练习册系列答案
相关题目
抛物线2x2+y=0的焦点坐标是( )
A、(0,-
| ||
B、(0,-
| ||
C、(-
| ||
D、(-
|
《几何原本》的作者是( )
| A、欧几里得 | B、阿基米德 |
| C、阿波罗尼奥斯 | D、托勒玫 |
已知点P是抛物线y2=6x上的一个动点,则点P到点M(0,2)的距离与点P到该抛物线的准线的距离之和的最小值为( )
| A、2 | ||
| B、3 | ||
C、
| ||
D、
|
已知函数f(x)=
-mx+1的图象为曲线C,若曲线C存在与直线y=
x垂直的切线,则实数m的取值范围是( )
| e | x |
| 1 |
| 2 |
| A、m≤2 | ||
| B、m>2 | ||
C、m≤
| ||
D、m>-
|
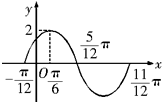 函数y=Asin(ωx+ϕ)
函数y=Asin(ωx+ϕ)