题目内容
7.若方程2sin2x+sinx-m-2=0在[0,2π)上有且只有两解,则实数m的取值范围是(-1,1)∪{-$\frac{17}{8}$}.分析 由题意可得函数y=2sin2x+sinx的图象和直线y=m+2在[0,2π)上有且只有两个交点,即函数y=2t2+t的图象和直线直线y=m+2在(-1,1)上有且只有一个交点,数形结合求得m的范围.
解答 解:由于方程2sin2x+sinx-m-2=0在[0,2π)上有且只有两解,
故函数y=2sin2x+sinx的图象和直线y=m+2在[0,2π)上有且只有两个交点.
由于sinx在(-1,1)上任意取一个值,在[0,2π)上都有2个x值和它对应,
故令t=sinx∈[-1,1],则函数y=2t2+t的图象和直线直线y=m+2在(-1,1)上有且只有一个交点,
如图所示:∵当t=-$\frac{1}{4}$时,y=-$\frac{1}{8}$,
故 1<m+2<3或m+2=-$\frac{1}{8}$,求得-1<m<1或m=-$\frac{17}{8}$,
故答案为:(-1,1)∪{-$\frac{17}{8}$}.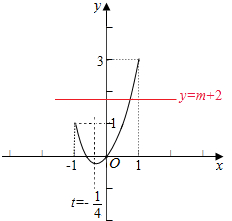
点评 本题主要考查正弦函数的值域,二次函数的性质,方程根的存在性以及个数判断,属于中档题.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
18.直线a与直线b无公共点,则( )
| A. | a∥b | B. | a,b异面 | C. | a∥b或a,b异面 | D. | 以上答案都不对 |
16.已知平面α内的三点A(0,0,1)、B(0,1,0)、C(1,0,0),平面β的一个法向量为(-1,-1,-1),且β与α不重合( )
| A. | α∥β | B. | α⊥β | ||
| C. | α与β相交但不垂直 | D. | 以上都不对 |