题目内容
2.某公路段在某一时刻内监测到的车速频率分布直方图如图所示.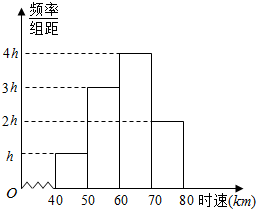
(1)求纵坐标中h的值及车速在[60,70)的频率;
(2)求车速的中位数v的估计值;
(3)求平均车速的估计值.
分析 (1)根据频率和为1,列出方程求出h的值,再计算车速在[60,70)的概率;
(2)根据车速的中位数两边直方图的面积相等,求出中位数v的值;
(3)根据频率分布直方图,求出平均车速.
解答 解:(1)因为所有小长方形的面积之和为1,
所以10h+10×3h+10×4h+10×2h=1,
解得h=0.01,
所以车速在[60,70)的概率为10×4h=0.4;
(2)车速的中位数两边直方图的面积相等,于是得:
10×0.01+10×0.03+(v-60)×0.04=0.5,
解得v=62.5(km/h);
(3)根据频率分布直方图,求平均车速为
0.01×10×45+0.03×10×55+0.04×10×65+0.02×10×75=62(km/h).
点评 本题考查了利用频率分布直方图求中位数与平均数的应用问题,是基础题目.

练习册系列答案
相关题目
12.为评估设备M生产某种零件的性能,从设备M生产零件的流水线上随机抽取100件零件作为样本,测量其直径后,整理得到下表:
经计算,样本的平均值μ=65,标准差σ=2.2,以频率值作为概率的估计值.
(Ⅰ)为证判一台设备的性能,从该设备加工的零件中任意抽取一件,记其直径为X,并根据以下不等式进行评判(P表示相就事件睥概率):①P(μ-σ<X≤μ+σ)≥0.6826,②P(μ-2σ<X≤μ+2σ)≥0.9544,③P(μ-3σ<X≤μ+3σ)≥0.9974,评判规则为:若同时满足上述三个不等式,则设备等级为甲;若仅满足其中两个,则等级为乙,若仅满足其中一个,则等级为丙;若全部都不满足,则等级为丁,试判定设备M的性能等级.
(Ⅱ)将直径小于等于μ-2σ或直径不大于μ+2σ的零件认为是次品,从样本所含次品中任取2件,则它们的直径之差不超过1mm的概率是多少?
| 直径/mm | 58 | 59 | 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 | 71 | 73 | 合计 |
| 件数 | 1 | 1 | 3 | 5 | 6 | 19 | 33 | 18 | 4 | 4 | 2 | 1 | 2 | 1 | 100 |
(Ⅰ)为证判一台设备的性能,从该设备加工的零件中任意抽取一件,记其直径为X,并根据以下不等式进行评判(P表示相就事件睥概率):①P(μ-σ<X≤μ+σ)≥0.6826,②P(μ-2σ<X≤μ+2σ)≥0.9544,③P(μ-3σ<X≤μ+3σ)≥0.9974,评判规则为:若同时满足上述三个不等式,则设备等级为甲;若仅满足其中两个,则等级为乙,若仅满足其中一个,则等级为丙;若全部都不满足,则等级为丁,试判定设备M的性能等级.
(Ⅱ)将直径小于等于μ-2σ或直径不大于μ+2σ的零件认为是次品,从样本所含次品中任取2件,则它们的直径之差不超过1mm的概率是多少?
13.下列命题错误的是( )
| A. | 命题“若m>0,则方程x2+x-m=0有实根”的逆否命题为:“若方程x2+x-m=0无实根,则m≤0” | |
| B. | 若p∧q为假命题,则p,q均为假命题 | |
| C. | “x=1”是“x2-3x+2=0”的充分不必要条件 | |
| D. | 若椭圆$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{25}$=1的两焦点为F1、F2,且弦AB过F1点,则△ABF2的周长为20 |
10.已知复数z满足zi=1,则|z|=( )
| A. | $\sqrt{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 1 | D. | $\frac{1}{2}$ |
17.在△ABC中,a=2$\sqrt{3}$,c=2$\sqrt{2}$,A=60°,则C=( )
| A. | 30° | B. | 45° | C. | 45°或135° | D. | 60° |
7.定义平面上一点P到曲线C的距离为点P到曲线C上所有点距离的最小值,那么平面内到定圆的距离与到定点A的距离相等的点的轨迹不可能是( )
| A. | 圆 | B. | 椭圆 | C. | 双曲线的一支 | D. | 直线 |
11.下列等式中恒成立的是( )
| A. | $sinαcos(α+\frac{π}{6})-cosαsin(α+\frac{π}{6})=-\frac{1}{2}$ | B. | $tan(α+\frac{π}{4})=\frac{1-tanα}{1+tanα}$ | ||
| C. | $sin(α+\frac{π}{4})=sinα+cosα$ | D. | sinαcosα=sinα |
