题目内容
已知f(x)=ex-ax-1(a∈R),求证:对于任意的a∈R,总存在x0∈[0,+∞),使得f(x0)>0.
考点:函数的最值及其几何意义
专题:函数的性质及应用
分析:f(0)=e0-a×0-1=0,当a≤0时,函数f(x)=ex-ax-1在R上递增,由x>0时,得f(x)>0,满足要求;
当a>0时,画y=ex与y=ax+1的图象,从图象来做题.
当a>0时,画y=ex与y=ax+1的图象,从图象来做题.
解答:
解:(1)f(0)=e0-a×0-1=0,
当a≤0时,函数f(x)=ex-ax-1在R上递增,∴x>0时,f(x)>0,满足要求;
当a>0时,f(x0)>0,即ex0-ax0-1>0即ex0>ax0+1,
画y=ex与y=ax+1的图象:
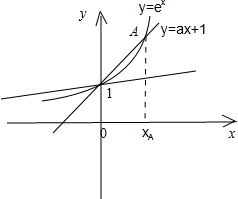
从图象上看,不论直线y=ax+1与y=ex相切、相交,总有x0>xA时,满足f(x0)>0,满足ex0>ax0+1,
综上,对于任意的a∈R,总存在x0∈[0,+∞),使得f(x0)>0.
当a≤0时,函数f(x)=ex-ax-1在R上递增,∴x>0时,f(x)>0,满足要求;
当a>0时,f(x0)>0,即ex0-ax0-1>0即ex0>ax0+1,
画y=ex与y=ax+1的图象:
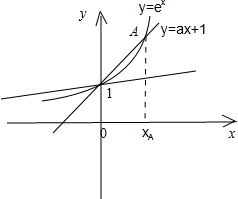
从图象上看,不论直线y=ax+1与y=ex相切、相交,总有x0>xA时,满足f(x0)>0,满足ex0>ax0+1,
综上,对于任意的a∈R,总存在x0∈[0,+∞),使得f(x0)>0.
点评:本题主要考查函数图象的应用,不等式的问题常转化为两个函数的函数值的比较.

练习册系列答案
相关题目
若-b<a<0,且函数f(x)的定义域是[a,b],则函数F(x)=f(x)+f(-x)的定义域是( )
| A、[a,b] |
| B、[-b,-a] |
| C、[-b,b] |
| D、[a,-a] |
下列有关命题的说法正确的是( )
| A、命题“若α=β,则sinα=sinβ”的逆命题为真命题 | ||
| B、已知命题p:函数f(x)=tanx的定义域为{x|x≠kπ,k∈Z},命题q:?x∈R,x2-x+1≥0;则命题p∧q为真命题 | ||
C、“a=2”是“直线y=-ax+2与直线y=
| ||
| D、命题“?x∈R,使得x2+2x+3<0”的否定形式是真命题 |
 已知点F(0,2)是抛物线x2=ay的焦点.
已知点F(0,2)是抛物线x2=ay的焦点.