题目内容
若-b＜a＜0，且函数f（x）的定义域是[a，b]，则函数F（x）=f（x）+f（-x）的定义域是（ ）
| A、[a，b] |
| B、[-b，-a] |
| C、[-b，b] |
| D、[a，-a] |
考点：函数的定义域及其求法
专题：函数的性质及应用
分析：先根据函数f（x）的定义域为[a，b]，求出f（-x）中x的范围，而函数F（x）=f（x）-f（-x）的定义域，为f（x）中x的范围与f（-x）中x的范围的交集，再根据-b＜a＜0，取交集即可．
解答：
解：∵函数f（x）的定义域为[a，b]，
∴f（-x）中a≤-x≤b，即-b≤x≤-a
∴函数F（x）=f（x）-f（-x）要成立，需满足
，
∴a≤x≤-a
故函数F（x）=f（x）-f（-x）的定义域是[a，-a]
故选：D．
∴f（-x）中a≤-x≤b，即-b≤x≤-a
∴函数F（x）=f（x）-f（-x）要成立，需满足
|
∴a≤x≤-a
故函数F（x）=f（x）-f（-x）的定义域是[a，-a]
故选：D．
点评：本题主要考察了抽象函数的定义域的求法，属于常规题型．
练习册系列答案
名师点睛字词句段篇系列答案
相关题目
在下列各数中，最大的数是（ ）
| A、11111（2） |
| B、1000（4） |
| C、210（6） |
| D、85（9） |
已知点P是椭圆
+
=1上的一点，且以点P及焦点F1，F2为顶点的三角形的面积等于1，则这样的点P有（ ）
| x2 |
| 5 |
| y2 |
| 4 |
| A、1个 | B、2个 | C、3个 | D、4个 |
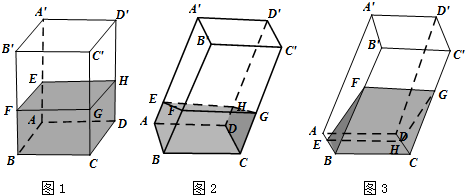
如图，试根据下列要求，把被遮挡的部分改为虚线．
如图，在矩形ABCD，AB=a，BC=1（a＞1），点E，F，G，H分别在边AB、BC、CD、DA上，且有BE=BF=DG=DH=x