题目内容
a，b＞0，a+b=4，则（a+
）2+（b+
）2的最小值是 ．
| 1 |
| a |
| 1 |
| b |
考点：基本不等式在最值问题中的应用
专题：不等式
分析：因为a+b=4，所以(a+
)2+(b+
)2=a2+b2+
+
+4=（a2+b2）+
(a+b)2(
+
)+4=（a2+b2）+
(
+
+
+
+2)+4．因为a2+b2≥2ab，
+
≥4，
+
≥2，并且都是a=b时取“=”，所以此时a=b=2，所以便得到(a+
)2+(b+
)2的最小值为
．
| 1 |
| a |
| 1 |
| b |
| 1 |
| a2 |
| 1 |
| b2 |
| 1 |
| 16 |
| 1 |
| a2 |
| 1 |
| b2 |
| 1 |
| 16 |
| 2b |
| a |
| 2a |
| b |
| b2 |
| a2 |
| a2 |
| b2 |
| 2b |
| a |
| 2a |
| b |
| b2 |
| a2 |
| a2 |
| b2 |
| 1 |
| a |
| 1 |
| b |
| 25 |
| 2 |
解答：
解：(a+
)2+(b+
)2=a2+b2+
+
+4=(a2+b2)+
(a+b)2(
+
)+4=(a2+b2)+
(
+
+
+
+2)+4；
∵a2+b2≥2ab，
+
≥4，
+
≥2，都是a=b时取“=”；
∵a+b=4，∴此时a=b=2；
∴(a2+b2)+
(
+
+
+
)+48+
(4+2+2)+4=
；
∴(a+
)2+(b+
)2的最小值是
；
故答案为：
．
| 1 |
| a |
| 1 |
| b |
| 1 |
| a2 |
| 1 |
| b2 |
| 1 |
| 16 |
| 1 |
| a2 |
| 1 |
| b2 |
| 1 |
| 16 |
| 2b |
| a |
| 2a |
| b |
| b2 |
| a2 |
| a2 |
| b2 |
∵a2+b2≥2ab，
| 2b |
| a |
| 2a |
| b |
| b2 |
| a2 |
| a2 |
| b2 |
∵a+b=4，∴此时a=b=2；
∴(a2+b2)+
| 1 |
| 16 |
| 2b |
| a |
| 2a |
| b |
| b2 |
| a2 |
| a2 |
| b2 |
| 1 |
| 16 |
| 25 |
| 2 |
∴(a+
| 1 |
| a |
| 1 |
| b |
| 25 |
| 2 |
故答案为：
| 25 |
| 2 |
点评：考查基本不等式：a2+b2≥2ab，a+b≥2
，a＞0，b＞0，的运用，并注意等号成立的条件．
| ab |
练习册系列答案
名校课堂系列答案
相关题目
设集合A={1，2}，则满足A∪B={1，2，3}的集合B的个数是（ ）
| A、1个 | B、2个 | C、4个 | D、8个 |
在下列各数中，最大的数是（ ）
| A、11111（2） |
| B、1000（4） |
| C、210（6） |
| D、85（9） |
函数f（x）=lg（x-1）+
的定义域是（ ）
| 3-x |
| A、（1，3） |
| B、[1，3] |
| C、（1，3] |
| D、[1，3） |
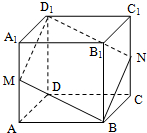在正方体ABCD-A1B1C1D1 中，过对角线BD1 的一个平面交AA1 于M，交CC1 于N．给出下列四个结论：