题目内容
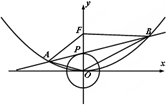 已知点F(0,2)是抛物线x2=ay的焦点.
已知点F(0,2)是抛物线x2=ay的焦点.(1)求抛物线方程;
(2)若点P(x0,y0)为圆x2+y2=1上一动点,直线l是圆在点P处的切线,直线l与抛物线相交于A,B两点(A,B在y轴的两侧),求平面图形OAFB面积的最小值.
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:(1)利用点F(0,2)是抛物线x2=ay的焦点,求出a,即可求抛物线方程;
(2)确定0<y0<1,|x1-x2|≥4
,即可求平面图形OAFB面积的最小值.
(2)确定0<y0<1,|x1-x2|≥4
| 2 |
解答:
解:(1)∵点F(0,2)是抛物线x2=ay的焦点,
∴a=8,
∴抛物线方程为x2=8y….(2分)
(2)联立直线l与抛物线方程可得y0x2+8x0x-8=0,
由题意可得-
<0,故0<y0<1,…..(8分)
设点A(x1,y1),B(x2,y2).
则x1+x2=
,x1x2=-
,且x02+y02=1,…(10分)
∴|x1-x2|2=
+
=32[2(
+
)2-
]≥32,….(14分)
当且仅当y0=1时取“=”,
∴|x1-x2|≥4
,
∴S=
|OF||x1-x2|≥4
,…..(15分)
即平面图形OAFB面积的最小值为4
,…..(16分)
∴a=8,
∴抛物线方程为x2=8y….(2分)
(2)联立直线l与抛物线方程可得y0x2+8x0x-8=0,
由题意可得-
| 8 |
| y0 |
设点A(x1,y1),B(x2,y2).
则x1+x2=
| -8x0 |
| y0 |
| 8 |
| y0 |
∴|x1-x2|2=
| 64x02 |
| y02 |
| 32 |
| y0 |
| 1 |
| y0 |
| 1 |
| 4 |
| 17 |
| 8 |
当且仅当y0=1时取“=”,
∴|x1-x2|≥4
| 2 |
∴S=
| 1 |
| 2 |
| 2 |
即平面图形OAFB面积的最小值为4
| 2 |
点评:本题考查抛物线方程,考查直线与抛物线的位置关系,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
设集合A={1,2},则满足A∪B={1,2,3}的集合B的个数是( )
| A、1个 | B、2个 | C、4个 | D、8个 |
已知点P是椭圆
+
=1上的一点,且以点P及焦点F1,F2为顶点的三角形的面积等于1,则这样的点P有( )
| x2 |
| 5 |
| y2 |
| 4 |
| A、1个 | B、2个 | C、3个 | D、4个 |
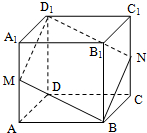 在正方体ABCD-A1B1C1D1 中,过对角线BD1 的一个平面交AA1 于M,交CC1 于N.给出下列四个结论:
在正方体ABCD-A1B1C1D1 中,过对角线BD1 的一个平面交AA1 于M,交CC1 于N.给出下列四个结论:
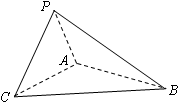 如图,平面PAC⊥平面ABC,△PAC是正三角形,∠CAB=90°,AB=2AC.
如图,平面PAC⊥平面ABC,△PAC是正三角形,∠CAB=90°,AB=2AC.