题目内容
设点P是不等式
表示的平面区域内D内的一点,点Q是圆C1:x2+y2-8x+2y+12+m=0上的一点,且平面区域D在圆C外,若线段PQ长的最大值小于3
,最小值大于
,则实数m的取值范围( )
|
| 5 |
| ||
| 2 |
| A、(-1,1) | ||
B、(
| ||
C、(
| ||
D、(
|
考点:简单线性规划的应用
专题:计算题,作图题,不等式的解法及应用
分析:由题意化简x2+y2-8x+2y+12+m=0为(x-4)2+(y+1)2=5-m;作出平面区域,从而可得线段PQ长的最大值为
+
<3
;线段PQ长的最小值为
-
>
;从而求解.
| 42+(1+1)2 |
| 5-m |
| 5 |
| 10 |
| 5-m |
| ||
| 2 |
解答:
解:化简x2+y2-8x+2y+12+m=0为(x-4)2+(y+1)2=5-m;
由题意作出其平面区域,
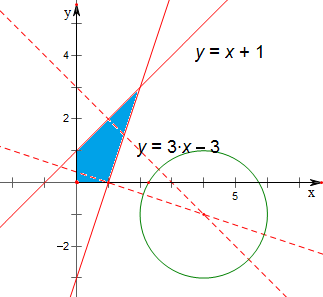
圆心到直线y=3x-3的距离为圆心到点(1,0)的距离为
;
圆心到直线y=x+1的距离为
=3
;
线段PQ长的最大值为
+
<3
;
线段PQ长的最小值为
-
>
;
解得
<m<5;
故选D.
由题意作出其平面区域,

圆心到直线y=3x-3的距离为圆心到点(1,0)的距离为
| 10 |
圆心到直线y=x+1的距离为
| |4+1+1| | ||
|
| 2 |
线段PQ长的最大值为
| 42+(1+1)2 |
| 5-m |
| 5 |
线段PQ长的最小值为
| 10 |
| 5-m |
| ||
| 2 |
解得
| 5 |
| 2 |
故选D.
点评:本题考查了简单线性规划,作图要细致认真,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目