题目内容
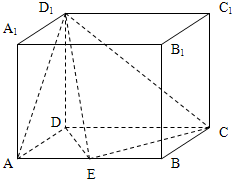 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E是AB上的点,若直线D1E与EC垂直,
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E是AB上的点,若直线D1E与EC垂直,(Ⅰ)求线段AE的长;
(Ⅱ)求二面角D1-EC-D的大小;
(Ⅲ)求D点到平面CD1E的距离.
考点:用空间向量求平面间的夹角,点、线、面间的距离计算,二面角的平面角及求法
专题:空间位置关系与距离,空间角
分析:(Ⅰ)解法一:证明DE与CE垂直,设AE=a,在直角三角形△DEC中,DC2=DE2+CE2,求得AE.
解法二:利用向量法.分别以DA,DC,DD1所在的直线为x、y、z轴如图建立坐标系.设AE=a,写出A;E;C; D1.则
=(1,a,-1),
=(1,a-2,0),利用
•
=1+a(a-2)=0,求得AE.
(Ⅱ)解法一:说明∠D1ED是所求二面角D1-EC-D的平面角,在RT△D1ED中,求解二面角D1-EC-D即可.
解法二:利用向量法.求出平面CD1E的法向量,平面CDE的法向量利用向量的数量积求解二面角D1-EC-D.
(Ⅲ))解法一:求出S△CDE=
×
×
=1以及S△CDE=
×
×
=
,设D点到平面CD1E的距离为d,利用VD1-CDE=VD-CD1E,求解D点到平面CD1E的距离.
解法二:利用向量法.求出
=(1,1,0),平面CD1E的法向量,利用向量的数量积求解D点到平面CD1E的距离.
解法二:利用向量法.分别以DA,DC,DD1所在的直线为x、y、z轴如图建立坐标系.设AE=a,写出A;E;C; D1.则
| D1E |
| CE |
| D1E |
| CE |
(Ⅱ)解法一:说明∠D1ED是所求二面角D1-EC-D的平面角,在RT△D1ED中,求解二面角D1-EC-D即可.
解法二:利用向量法.求出平面CD1E的法向量,平面CDE的法向量利用向量的数量积求解二面角D1-EC-D.
(Ⅲ))解法一:求出S△CDE=
| 1 |
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| ||
| 2 |
解法二:利用向量法.求出
| DE |
解答:
 解:(Ⅰ)解法一:由直线D1E与EC垂直,及DD1⊥平面ABCD
解:(Ⅰ)解法一:由直线D1E与EC垂直,及DD1⊥平面ABCD
⇒DE与CE垂直
设AE=a,则DE=
,CE=
,又知DC=2…(2分)
在直角三角形△DEC中,DC2=DE2+CE2,求得AE=a=1…(4分)
解法二:利用向量法
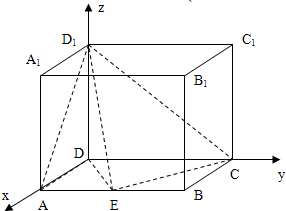
分别以DA,DC,DD1所在的
直线为x、y、z轴如图建立坐标系.
设AE=a,写出坐标:
A(1,0,0); E(1,a,0 );
C (0,2,0); D1(0,0,1);…(1分)
则
=(1,a,-1),
=(1,a-2,0)∵
⊥
…(2分)
∴
•
=1+a(a-2)=0,求得AE=a=1.…(4分)
(Ⅱ)解法一:由D1E与EC垂直⇒DE与CE垂直,
所以∠D1ED是所求二面角D1-EC-D的平面角…(5分)
在RT△D1ED中,DD1=1,DE=
;
故,tan∠D1ED=
=
…(7分)
二面角D1-EC-D是arctan
.…(8分)
解法二:利用向量法
设平面CD1E的法向量为
=(x,y,1),
由(Ⅰ)得
=(1,1,-1),
=(1,-1,0)
•
=x+y-1=0且
•
=x-y=0
解得:x=y=
,即
=(
,
,1);…(6分)
又平面CDE的法向量为
=(0,0,1),∴cos?
,
>=
=
=
.
故,二面角D1-EC-D是arccos
.…(8分)
(Ⅲ))解法一:∵DE=CE=
,DE⊥CE,∴S△CDE=
×
×
=1…(9分)
又∵D1E=
,D1E⊥CE,∴S△CDE=
×
×
=
…(10分)
设D点到平面CD1E的距离为d,则VD1-CDE=
×1×1=VD-CD1E=
×
×d,
解得d=
,即D点到平面CD1E的距离为
.…(12分)
解法二:利用向量法
由(Ⅰ) (Ⅱ)得
=(1,1,0),
平面CD1E的法向量为
=(
,
,1)
故,D点到平面CD1E的距离为d=
=
=
.…(12分)
 解:(Ⅰ)解法一:由直线D1E与EC垂直,及DD1⊥平面ABCD
解:(Ⅰ)解法一:由直线D1E与EC垂直,及DD1⊥平面ABCD⇒DE与CE垂直
设AE=a,则DE=
| 1+a2 |
| 1+(2-a)2 |
在直角三角形△DEC中,DC2=DE2+CE2,求得AE=a=1…(4分)
解法二:利用向量法
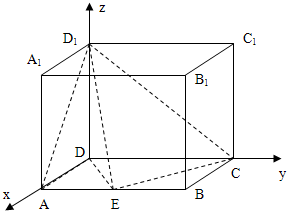
分别以DA,DC,DD1所在的
直线为x、y、z轴如图建立坐标系.
设AE=a,写出坐标:
A(1,0,0); E(1,a,0 );
C (0,2,0); D1(0,0,1);…(1分)
则
| D1E |
| CE |
| D1E |
| CE |
∴
| D1E |
| CE |
(Ⅱ)解法一:由D1E与EC垂直⇒DE与CE垂直,
所以∠D1ED是所求二面角D1-EC-D的平面角…(5分)
在RT△D1ED中,DD1=1,DE=
| 2 |
故,tan∠D1ED=
| 1 | ||
|
| ||
| 2 |
二面角D1-EC-D是arctan
| ||
| 2 |
解法二:利用向量法
设平面CD1E的法向量为
| m |
由(Ⅰ)得
| D1E |
| CE |
| m |
| D1E |
| m |
| CE |
解得:x=y=
| 1 |
| 2 |
| m |
| 1 |
| 2 |
| 1 |
| 2 |
又平面CDE的法向量为
| DD1 |
| m |
| DD1 |
| ||||
|
|
| 1 | ||||||
|
| ||
| 3 |
故,二面角D1-EC-D是arccos
| ||
| 3 |
(Ⅲ))解法一:∵DE=CE=
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
又∵D1E=
| 3 |
| 1 |
| 2 |
| 3 |
| 2 |
| ||
| 2 |
设D点到平面CD1E的距离为d,则VD1-CDE=
| 1 |
| 3 |
| 1 |
| 3 |
| ||
| 2 |
解得d=
| ||
| 3 |
| ||
| 3 |
解法二:利用向量法
由(Ⅰ) (Ⅱ)得
| DE |
平面CD1E的法向量为
| m |
| 1 |
| 2 |
| 1 |
| 2 |
故,D点到平面CD1E的距离为d=
|
| ||||
|
|
| ||||
|
| ||
| 3 |

点评:本题考查二面角的求法,点到平面的距离的求法,空间两点之间距离的求法,本题利用几何法以及向量法求解,注意学习与掌握.

练习册系列答案
相关题目
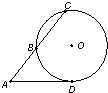 如图,从圆O外一点A引圆的切线AD和割线ABC,已知AD=4
如图,从圆O外一点A引圆的切线AD和割线ABC,已知AD=4