题目内容
已知双曲线的一条准线与两渐近线的交点分别为A、B,相应于这条准线的焦点为F,如果△ABF是等边三角形,那么双曲线的离心率为( )
A、
| ||||
| B、2 | ||||
| C、4 | ||||
D、
|
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:根据双曲线的渐近线方程和准线方程公式,算出右准线交渐近线于A,B的坐标.根据△AFB为等边三角形,建立关于a、b、c的方程,化简算出
a=b,从而得到双曲线的离心率e=2.
| 3 |
解答:
解:∵双曲线
-
=1的准线方程为x=±
,渐近线方程为y=±
x,
∴以右准线为例,求得它与两条渐近线交于A、B两点,
得A(
,
),B(
,-
)
由于△ABF是等边三角形,F(c,0),
∴c-
=
|AB|=
,即
=
,化简得
a=b
因此,c=
=2a,
双曲线的离心率e=
=2.
故选B.
| x2 |
| a2 |
| y2 |
| b2 |
| a2 |
| c |
| b |
| a |
∴以右准线为例,求得它与两条渐近线交于A、B两点,
得A(
| a2 |
| c |
| ab |
| c |
| a2 |
| c |
| ab |
| c |
由于△ABF是等边三角形,F(c,0),
∴c-
| a2 |
| c |
| ||
| 2 |
| ||
| c |
| c2-a2 |
| c |
| ||
| c |
| 3 |
因此,c=
| a2+b2 |
双曲线的离心率e=
| c |
| a |
故选B.
点评:本题给出双曲线满足的条件,求双曲线的离心率.着重考查了三角形的形状判断、双曲线的标准方程与简单几何性质等知识,属于中档题.

练习册系列答案
相关题目
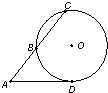 如图,从圆O外一点A引圆的切线AD和割线ABC,已知AD=4
如图,从圆O外一点A引圆的切线AD和割线ABC,已知AD=4