题目内容
已知，正方形ABCD的边长为1，AP⊥平面ABCD，且AP=
，则PC与平面PAB所成的角是 ．
| 2 |
考点：直线与平面所成的角
专题：空间角
分析：画出图形，利用已知判断BC⊥平面PAB，找到PC与平面PAB所成的角，然后通过解直角三角形求大小．
解答：
解：如图，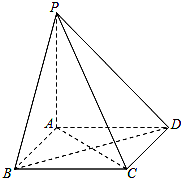
因为底面是正方形，AP⊥平面ABCD，
所以AP⊥BC，又BC⊥AB，
所以BC⊥平面PAB，
所以∠BPC为PC与平面PAB所成的角，
正方形ABCD的边长为1，AP=
，
所以PB=
=
，
tan∠BPC=
=
=
，
所以∠BPC=
．
因为底面是正方形，AP⊥平面ABCD，所以AP⊥BC，又BC⊥AB，
所以BC⊥平面PAB，
所以∠BPC为PC与平面PAB所成的角，
正方形ABCD的边长为1，AP=
| 2 |
所以PB=
| PA2+AB2 |
| 3 |
tan∠BPC=
| BC |
| PB |
| 1 | ||
|
| ||
| 3 |
所以∠BPC=
| π |
| 6 |
点评：本题考查了线面垂直的性质、判定以及线面角的求法，关键是找到角所在，然后解三角形计算．
练习册系列答案
夺冠训练单元期末冲刺100分系列答案
新思维小冠军100分作业本系列答案
名师指导一卷通系列答案
相关题目
已知双曲线x2-
=1的左顶点为A1，右焦点为F2，P为双曲线右支上一点，则
•
最小值为（ ）
| y2 |
| 3 |
| PA1 |
| PF2 |
| A、-2 | ||
B、-
| ||
| C、1 | ||
| D、0 |