Question

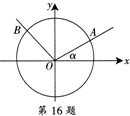如图，角α的始边与x轴的非负半轴重合，终边与单位圆交于点A （x₁，y_l），将射线OA按逆时针方向旋转

2π

3

后与单位圆交于点B（x₂，y₂），f（a）=x_l-x₂．
（Ⅰ）若角α为锐角，求f（α）的取值范围；
（Ⅱ）比较f（2）与f（3）的大小．

Answer 1

考点：任意角的三角函数的定义,象限角、轴线角

专题：三角函数的求值

分析：（Ⅰ）由三角函数的定义可得 x₁=cosα，x₂=cos（α+

2π

3

），化简f（a）为

3

sin（α+

π

3

）．根据 

π

3

＜α+

π

3

＜

5π

6

，利用正弦函数的定义域和值域求得f（α）的范围．
（Ⅱ）根据f（2）=

3

sin（2+

π

3

），f（3）=

3

sin（3+

π

3

），函数y=sinx在（

π

2

，

3π

2

）上是减函数，从而得出结论．

解答： 解：（Ⅰ）如图所示，∠AOB=

2π

3

，由三角函数的定义可得 x₁=cosα，x₂=cos（α+

2π

3

），
f（α）=x_l-x₂ =cosα-cos（α+

2π

3

）=cosα-cosαcos

2π

3

+sinαsin

2π

3

=

3

2

cosα+

3

2

sinα
=

3

sin（α+

π

3

）．
∵角α为锐角，∴

π

3

＜α+

π

3

＜

5π

6

，∴

1

2

＜sin（α+

π

3

）≤1，
∴

3

2

＜

3

sin（α+

π

3

）≤

3

，即f（α）的范围是（

3

2

，

3

]．
（Ⅱ）∵f（2）=

3

sin（2+

π

3

），f（3）=

3

sin（3+

π

3

），

π

2

＜2+

π

3

＜3+

π

3

＜

3π

2

，函数y=sinx在（

π

2

，

3π

2

）上是减函数，
∴f（2）＞f（3）．

点评：本题主要考查任意角的三角函数的定义，正弦函数的定义域和值域、单调性，属于中档题．