题目内容
已知函数f(x)=sin2ωx+
sinωsin(ωx+
)+2cos2ωx,x∈R(ω>0),在y轴右侧的第一个最高点的横坐标为
.若将函数f(x)的图象向右平移
个单位后,再将得到的图象上各点横坐标伸长到原来的2倍,纵坐标不变,得到函数y=g(x)的图象.
(1)求函数g(x)的最大值及单调递减区间.
(2)(理)在△ABC中,a,b,c分别是角A,B,C的对边,a=
,b+c=3,且f(A)=2,求△ABC的面积.
| 3 |
| π |
| 2 |
| π |
| 6 |
| π |
| 6 |
(1)求函数g(x)的最大值及单调递减区间.
(2)(理)在△ABC中,a,b,c分别是角A,B,C的对边,a=
| 3 |
考点:正弦定理,函数y=Asin(ωx+φ)的图象变换
专题:解三角形
分析:(1)利用辅助角公式和倍角公式将函数化简f(x)=sin(2ωx+
)+
,再根据题设条件求出ω=1,然后根据条件进行变换即可;
(2)(理)根据f(A)=2确定A=
,利用余弦定理建立方程求解b、c,代入面积公式计算即可.
| π |
| 6 |
| 3 |
| 2 |
(2)(理)根据f(A)=2确定A=
| π |
| 3 |
解答:
解:(1)f(x)=sin2ωx+
sinωsin(ωx+
)+2cos2ωx
=
sin2ωx+
cos2ωx+
=sin(2ωx+
)+
.
令2ωx+
=
,
将x=
代入可得:ω=1.
∴f(x)=sin(2x+
)+
.
经过题设的变化得到的函数g(x)=sin(x-
)+
.
当x=2kπ+
π,k∈Z时,函数取得最大值
.
令2kπ+
≤x-
≤2kπ+
π,
即x∈[2kπ+
π,2kπ+
π],k∈Z为函数的单调递减区间.
(2)(理)f(x)=sin(2x+
)+
,
∵f(A)=2,
∴sin(2A+
)=
,
而
<2A+
<
π,
∴2A+
=
π,∴A=
,
由余弦定理知cosA=
,
∴b2+c2-bc=3,又b+c=3,
联立解得
或
,
∴S△ABC=
bcsinA=
.
| 3 |
| π |
| 2 |
=
| ||
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
=sin(2ωx+
| π |
| 6 |
| 3 |
| 2 |
令2ωx+
| π |
| 6 |
| π |
| 2 |
将x=
| π |
| 6 |
∴f(x)=sin(2x+
| π |
| 6 |
| 3 |
| 2 |
经过题设的变化得到的函数g(x)=sin(x-
| π |
| 6 |
| 3 |
| 2 |
当x=2kπ+
| 2 |
| 3 |
| 5 |
| 2 |
令2kπ+
| π |
| 2 |
| π |
| 6 |
| 3 |
| 2 |
即x∈[2kπ+
| 2 |
| 3 |
| 5 |
| 3 |
(2)(理)f(x)=sin(2x+
| π |
| 6 |
| 3 |
| 2 |
∵f(A)=2,
∴sin(2A+
| π |
| 6 |
| 1 |
| 2 |
而
| π |
| 6 |
| π |
| 6 |
| 13 |
| 6 |
∴2A+
| π |
| 6 |
| 5 |
| 6 |
| π |
| 3 |
由余弦定理知cosA=
| b2+c2-a2 |
| 2bc |
∴b2+c2-bc=3,又b+c=3,
联立解得
|
|
∴S△ABC=
| 1 |
| 2 |
| ||
| 2 |
点评:本题考查倍角公式、辅助角公式等三角恒等变换公式的应用,三角函数单调性,解三角形等基础知识的综合应用,属于中档题.

练习册系列答案
相关题目
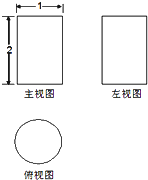 一个空间几何体的主视图和左视图都是矩形,俯视图是一个圆,尺寸如图,那么这个几何体的外接球的体积为( )
一个空间几何体的主视图和左视图都是矩形,俯视图是一个圆,尺寸如图,那么这个几何体的外接球的体积为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知双曲线C1:
-
=1(a>0,b>0)的离心率为
,一条渐近线为l,抛物线C2:y2=4x的焦点为F,点P为直线l与抛物线C2异于原点的交点,则|PF|=( )
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
| A、2 | B、3 | C、4 | D、5 |
三棱锥P-ABC中,PA、PB、PC两两垂直且PA=2
,PB=4,PC=2
,如果三棱锥的四个顶点都在同一球面上,那么这个球的体积等于( )
| 2 |
| 3 |
| A、36π | B、72π |
| C、144π | D、288π |
已知全集U={1,2,3,4,5},集合A={1,3,4},集合B={2,4},则(∁UA)∪B为( )
| A、{2,4,5} |
| B、{1,3,4} |
| C、{1,2,4} |
| D、{2,3,4,5} |
 已知算法如图:
已知算法如图: