题目内容
18.已知函数f(x)=2sin(3x+2φ)为偶函数,则φ的最小正值为$\frac{π}{4}$.分析 利用函数是偶函数,求出φ的表达式,然后求解最小正值.
解答 解:由题意,$2φ=kπ+\frac{π}{2}({k∈{Z}})$,所以$φ=\frac{kπ}{2}+\frac{π}{4}({k∈{Z}})$.所以当k=0时,φ取得最小正值$\frac{π}{4}$.
故答案为:$\frac{π}{4}$.
点评 本题考查三角函数的奇偶性的应用,考查计算能力.

练习册系列答案
相关题目
13.在等差数列中,若a2=3,a7=13,则数列{an}的前8项和是( )
| A. | 56 | B. | 64 | C. | 80 | D. | 128 |
3.已知集合A={1,m2},B={0,4},则“m=-2”是“A∩B={4}”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
10.已知四边形ABCD是平行四边形,对角线相交于点O,则下列等式中成立的是( )
| A. | $\overrightarrow{BC}$+$\overrightarrow{BA}$=$\overrightarrow{AC}$ | B. | $\overrightarrow{AB}$-$\overrightarrow{AC}$=$\overrightarrow{BC}$ | C. | $\overrightarrow{AO}$=$\frac{1}{2}$($\overrightarrow{AB}$+$\overrightarrow{AD}$) | D. | $\overrightarrow{AD}$=$\overrightarrow{CB}$ |
7.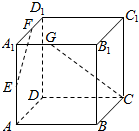 如图,在正方体ABCD-A1B1C1D1中,E、F、G分别是AA1,A1D1,A1B1的中点,则异面直线EF与CG所成的角等于( )
如图,在正方体ABCD-A1B1C1D1中,E、F、G分别是AA1,A1D1,A1B1的中点,则异面直线EF与CG所成的角等于( )
 如图,在正方体ABCD-A1B1C1D1中,E、F、G分别是AA1,A1D1,A1B1的中点,则异面直线EF与CG所成的角等于( )
如图,在正方体ABCD-A1B1C1D1中,E、F、G分别是AA1,A1D1,A1B1的中点,则异面直线EF与CG所成的角等于( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |