题目内容
13.在等差数列中,若a2=3,a7=13,则数列{an}的前8项和是( )| A. | 56 | B. | 64 | C. | 80 | D. | 128 |
分析 由等差数列通项公式列出方程组求出首项与公差,由此能求出数列{an}的前8项和.
解答 解:在等差数列中,
∵a2=3,a7=13,
∴$\left\{\begin{array}{l}{{a}_{1}+d=3}\\{{a}_{1}+6d=13}\end{array}\right.$,解得a1=1,d=2,
∴数列{an}的前8项和:
${S}_{8}=8{×1}_{\;}+\frac{8×7}{2}×2$=64.
故选:B.
点评 本题考查等差数列的前8项和的求法,是基础题,解题时要认真审题,注意等差数列的性质的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.已知体积为V的三棱柱ABC-A1B1C1,P为棱BB1上除B,B1两点外的任意一点,则四棱锥P-AA1C1C的体积等于( )
| A. | $\frac{V}{2}$ | B. | $\frac{V}{3}$ | C. | $\frac{2V}{3}$ | D. | $\frac{V}{4}$ |
8.已知函数f(ex)=x,则f(2)=( )
| A. | 2 | B. | e2 | C. | log2e | D. | ln2 |
5.下列结论中,正确的是( )
| A. | 三角形绕其一边旋转一周后成一个圆锥 | |
| B. | 一个直角梯形绕其一边旋转一周后成为一个圆台 | |
| C. | 平行四边形绕其一边旋转一周后成为圆柱 | |
| D. | 圆面绕其一条直径旋转一周后成为一个球 |
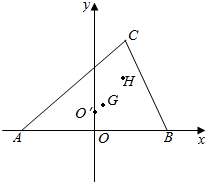 如图,A,B,C的坐标分别为(-$\frac{c}{2}$,0),($\frac{c}{2}$,0),(m,n),G,O′,H分别为△ABC的重心,外心,垂心.
如图,A,B,C的坐标分别为(-$\frac{c}{2}$,0),($\frac{c}{2}$,0),(m,n),G,O′,H分别为△ABC的重心,外心,垂心.