题目内容
8.f (x)是定义在R上的以2为周期的奇函数,f (3)=0,则函数y=f (x)在区间(-2,5)内的零点个数为( )| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
分析 根据函数奇偶性和周期性的关系结合函数函数零点的定义进行求解即可.
解答 解:∵f (x)是定义在R上的以2为周期的奇函数,f (3)=0,
∴f(x+2)=f(x),且f(-x)=-f(x),
则f(0)=0,f(2)=f(4)=f(0)=0,
f(-3)=-f (3)=0,
则f(-3+2)=f(1)=f(3)=0,
令x=-1得,f(-1+2)=f(-1),
即f(1)=-f(1),则f(1)=0,
则f(-1)=f(1)=f(3)=0,
故x=-1,0,1,2,3,4为函数f(x)的零点,
故函数y=f (x)在区间(-2,5)内的零点个数为6个,
故选:A
点评 本题主要考查函数零点的定义,结合函数奇偶性和周期性的关系进行转化递推是解决本题的关键.

练习册系列答案
 学习实践园地系列答案
学习实践园地系列答案
相关题目
17.已知集合M={x|$\frac{x-2}{x+1}$<0},N={x|x≤-1},则集合{x|x≥2}等于( )
| A. | M∩N | B. | M∪N | C. | ∁R(M∩N) | D. | ∁R(M∪N) |
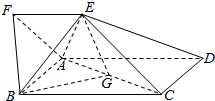 如图,四边形ABCD为矩形,四边形ADEF为梯形,AD∥FE,∠AFE=60°,且平面ABCD⊥平面ADEF,AF=FE=AB=$\frac{1}{2}AD$=2,点G为AC的中点.
如图,四边形ABCD为矩形,四边形ADEF为梯形,AD∥FE,∠AFE=60°,且平面ABCD⊥平面ADEF,AF=FE=AB=$\frac{1}{2}AD$=2,点G为AC的中点.