题目内容
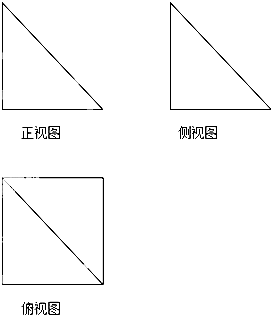一个几何体的三视图如图所示，其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形，若该几何体的所有顶点在同一球面上，则球的表面积是（ ）| A、3π | ||
| B、2π | ||
| C、π | ||
D、
|
考点：球的体积和表面积,球内接多面体
专题：空间位置关系与距离
分析：该几何体的直观图如图1所示，它是有一条侧棱垂直于底面的四棱锥．其中底面ABCD是边长为1的正方形，高为CC1=1，求出其外接球的半径，代入球的表面积公式，可得答案．
解答：
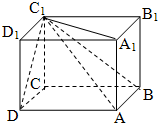解：该几何体的直观图如图1所示，它是有一条侧棱垂直于底面的四棱锥．
其中底面ABCD是边长为1的正方形，高为CC1=1，
该几何体的所有顶点都是棱长为1的正方体的顶点，
故几何体的外接球，即为棱长为1的正方体的外接球，
故球的直径R满足：2R=
=
，
∴R=
，
∴球的表面积是4π×（
）2=3π
故选：A
解：该几何体的直观图如图1所示，它是有一条侧棱垂直于底面的四棱锥．其中底面ABCD是边长为1的正方形，高为CC1=1，
该几何体的所有顶点都是棱长为1的正方体的顶点，
故几何体的外接球，即为棱长为1的正方体的外接球，
故球的直径R满足：2R=
| 12+12+12 |
| 3 |
∴R=
| ||
| 2 |
∴球的表面积是4π×（
| ||
| 2 |
故选：A
点评：本题考查三视图与直观图的关系，考查空间想象能力，考查学生的计算能力．
练习册系列答案
应用题点拨系列答案
状元及第系列答案
同步奥数系列答案
相关题目
已知点（-3，-1）和（4，-6）在直线3x-2y-a=0的两侧，则实数a的取值范围为（ ）
| A、（-24，7） |
| B、（-∞，-24）∪（7，+∞） |
| C、（-7，24） |
| D、（-∞，-7）∪（24，+∞） |
已知点M（a，b）（ab≠0）是圆x2+y2=r2内一点，直线g是以M为中点的弦所在直线，直线l的方程为ax+by+r2=0，则直线l（ ）
| A、l∥g，且与圆相切 |
| B、l∥g，且与圆相离 |
| C、l⊥g，且与圆相切 |
| D、l⊥g，且与圆相离 |
设关于x，y的不等式组
表示的平面区域内存在点P（x0，y0），满足x0-3y0=3，求得m的取值范围是（ ）
|
A、（-∞，-
| ||
B、（-∞，
| ||
C、（-∞，-
| ||
D、（-∞，
|
已知向量
，
均为单位向量，其夹角为θ，若|
-
|＜1，则θ的取值范围是（ ）
| a |
| b |
| a |
| b |
A、（0，
| ||
B、[0，
| ||
C、[0，
| ||
D、（
|
若a，b，c∈R，a＞b，则下列不等式成立的是（ ）
A、
| ||||
| B、a2＞b2 | ||||
C、
| ||||
| D、a|c|＞b|c| |