题目内容

已知点（-3，-1）和（4，-6）在直线3x-2y-a=0的两侧，则实数a的取值范围为（　　）
A、（-24，7）
B、（-∞，-24）∪（7，+∞）
C、（-7，24）
D、（-∞，-7）∪（24，+∞）
考点：直线的斜率
专题：直线与圆
分析：根据点（-3，-1）和（4，-6）在直线3x-2y-a=0的两侧，可得（-9+2-a）（12+12-a）＜0，解出即可．
解答： 解：∵点（-3，-1）和（4，-6）在直线3x-2y-a=0的两侧，
∴（-9+2-a）（12+12-a）＜0，
化为（a+7）（a-24）＜0，
解得-7＜a＜24．
故选：C．
点评：本题考查了线性规划的有关问题、一元二次不等式的解法，属于基础题．
练习册系列答案
相关题目
二次函数y=ax2+bx+c，若f（x1）=f（x2）（x1≠x2），则f(
x1+x2
2
)=
 
（用a、b、c表示）
化简
1-cos200°
=（　　）
A、-
2
cos100°
B、-
2
sin100°
C、
2
cos100°
D、
2
sin100°
对数lg(
3+
5
+
3-
5
)的值为（　　）
A、1
B、
1
2
C、2
D、
2
函数f（x）=
-x2+x
的单调递增区间为（　　）
A、[0，1]
B、（-∞，
1
2
]
C、[
1
2
，1]
D、[0，
1
2
]
对定义域分别是Df、Dg的函数y=f （x）、y=g （x），规定：h（x）=
f(x)•g(x)， 当x∈Df且x∈Dg
 f(x) ，当x∈Df且x∉Dg
 g(x) ，当x∉Df且x∈Dg.

（1）若函数f （x）=
1
x-1
，g （x）=x2，写出函数h（x）的解析式；
（2）求问题（1）中函数h（x）的值域；
（3）请设计一个定义域为R的函数y=f （x），及一个实常数a的值，使得f （x）•f （x+a）=x4+x2+1，并予证明．
某商品降价10%，经过一段时间后恢复原价，需提价
 
．
若关于x的方程ax2-2x+1=0的解集中有且仅有一个元素，则实数a的值组成的集合中的元素个数为（　　）
A、1B、2C、3D、4
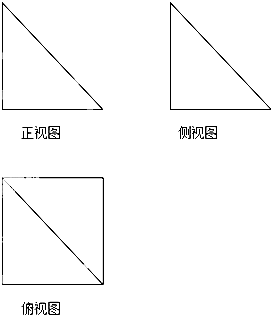一个几何体的三视图如图所示，其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形，若该几何体的所有顶点在同一球面上，则球的表面积是（　　）
A、3π
B、2π
C、π
D、
3π
2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网