题目内容
函数y=f(x)是定义在R上的函数,对任意实数x、y满足f(x)+f(y-x)=f(y),且当x>0时,f(x)<0.若对任意t∈(1,2),f(tx2-2x)<f(t+2)恒成立,求x的范围.
考点:函数恒成立问题,抽象函数及其应用
专题:函数的性质及应用,不等式的解法及应用
分析:由条件f(x)+f(y-x)=f(y),得出f(y-x)=f(y)-f(x),利用此恒等式推导函数为奇函数及单调递减函数,利用辩证思维,把t当自变量,x为常量解题,这样就把以x为自变量的复杂函数变成以t为自变量的一次函数处理,使问题简单化.
解答:
解:∵f(x)+f(y-x)=f(y),∴f(y-x)=f(y)-f(x),
令y=x代入上式得f(0)=f(x)-f(x),∴f(0)=0,
f(-x)=f(0-x)=f(0)-f(x)=0-f(x)=-f(x),∴f(x)为R上的奇函数.
设x1<x2,则f(x2)-f(x1)=f(x2-x1),
∵x2-x1>0,∴f(x2-x1)<0,∴f(x2)-f(x1)<0,
∴f(x2)<f(x1),∴f(x)为R上的减函数,
∴f(tx2-2x)<f(t+2)可化为tx2-2x>t+2,
∴tx2-2x-t-2>0,∴(x2-1)t-2x-2>0,
若对任意t∈(1,2),f(tx2-2x)<f(t+2)恒成立,即对任意t∈(1,2),(x2-1)t-2x-2>0,
令g(t)=(x2-1)t-2x-2,且g(t)是关于t的一次函数,
∴对任意t∈(1,2),g(t)>0,
∴①当x=1时,g(t)=-4,不满足g(t)>0,
②当x=-1时,g(t)=0,不满足g(t)>0,
③当x2>1时,即当x<-1,或x>1时,g(t)在(1,2)上递增,
∴g(1)>0,即x2-2x-3>0,解得x<-1,或x>3,
故当x2>1时,x的范围为x<-1,或x>3,
④当x2<1时,即当-1<x<1时,g(t)在(1,2)上递减,
∴g(2)>0,即2x2-2x-4>0,解得x<-1,或x>2,
故当x2<1时,x的范围为Φ,
综上①②③④x的范围为x<-1,或x>3,
令y=x代入上式得f(0)=f(x)-f(x),∴f(0)=0,
f(-x)=f(0-x)=f(0)-f(x)=0-f(x)=-f(x),∴f(x)为R上的奇函数.
设x1<x2,则f(x2)-f(x1)=f(x2-x1),
∵x2-x1>0,∴f(x2-x1)<0,∴f(x2)-f(x1)<0,
∴f(x2)<f(x1),∴f(x)为R上的减函数,
∴f(tx2-2x)<f(t+2)可化为tx2-2x>t+2,
∴tx2-2x-t-2>0,∴(x2-1)t-2x-2>0,
若对任意t∈(1,2),f(tx2-2x)<f(t+2)恒成立,即对任意t∈(1,2),(x2-1)t-2x-2>0,
令g(t)=(x2-1)t-2x-2,且g(t)是关于t的一次函数,
∴对任意t∈(1,2),g(t)>0,
∴①当x=1时,g(t)=-4,不满足g(t)>0,
②当x=-1时,g(t)=0,不满足g(t)>0,
③当x2>1时,即当x<-1,或x>1时,g(t)在(1,2)上递增,
∴g(1)>0,即x2-2x-3>0,解得x<-1,或x>3,
故当x2>1时,x的范围为x<-1,或x>3,
④当x2<1时,即当-1<x<1时,g(t)在(1,2)上递减,
∴g(2)>0,即2x2-2x-4>0,解得x<-1,或x>2,
故当x2<1时,x的范围为Φ,
综上①②③④x的范围为x<-1,或x>3,
点评:本题主要考查抽象函数的性质,也就是利用所给的函数的恒等式推导函数所具备的性质;另外,函数表达式中含有两个变量时,选择哪一个为自变量使问题简单化尤为重要.

练习册系列答案
相关题目
若关于x的方程ax2-2x+1=0的解集中有且仅有一个元素,则实数a的值组成的集合中的元素个数为( )
| A、1 | B、2 | C、3 | D、4 |
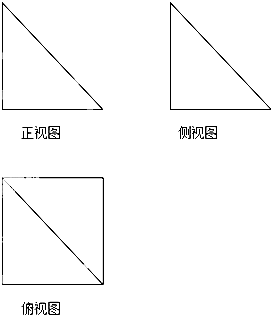 一个几何体的三视图如图所示,其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形,若该几何体的所有顶点在同一球面上,则球的表面积是( )
一个几何体的三视图如图所示,其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形,若该几何体的所有顶点在同一球面上,则球的表面积是( )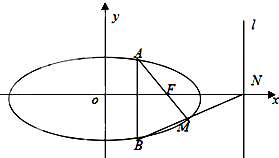 如图,已知直线x+ky-1=0所经过的定点F恰好是椭圆C的一个焦点,且椭圆C上的点到点F的最大距离为3.
如图,已知直线x+ky-1=0所经过的定点F恰好是椭圆C的一个焦点,且椭圆C上的点到点F的最大距离为3. 如图所示,某地一天从6~14时的温度变化曲线近似满足y=Asin(ωx+φ)+b(A>0,ω>0,|φ|<π,b∈R),写出这段曲线的函数解析式
如图所示,某地一天从6~14时的温度变化曲线近似满足y=Asin(ωx+φ)+b(A>0,ω>0,|φ|<π,b∈R),写出这段曲线的函数解析式